Geometry of Lattice Angles, Polygons, and Cones
... Lattice geometry. Geometry in general can be interpreted in many different ways. We take one of the classical definitions of geometry: geometry is a set of objects and a congruence relation for these objects. Usually a congruence relation is defined by some group of transformations. For instance in ...
... Lattice geometry. Geometry in general can be interpreted in many different ways. We take one of the classical definitions of geometry: geometry is a set of objects and a congruence relation for these objects. Usually a congruence relation is defined by some group of transformations. For instance in ...
LSU College Readiness Program COURSE
... Understand that two events A and B are independent if the probability of A and B occurring together is the product of their probabilities, and use this characterization to determine if they are independent. Understand the conditional probability of A given B as P(A and B)/P(B), and interpret indepen ...
... Understand that two events A and B are independent if the probability of A and B occurring together is the product of their probabilities, and use this characterization to determine if they are independent. Understand the conditional probability of A given B as P(A and B)/P(B), and interpret indepen ...
LSU College Readiness Program COURSE
... Understand that two events A and B are independent if the probability of A and B occurring together is the product of their probabilities, and use this characterization to determine if they are independent. Understand the conditional probability of A given B as P(A and B)/P(B), and interpret indepen ...
... Understand that two events A and B are independent if the probability of A and B occurring together is the product of their probabilities, and use this characterization to determine if they are independent. Understand the conditional probability of A given B as P(A and B)/P(B), and interpret indepen ...
Content, Methods, and Context of the Theory of Parallels
... critical acumen, was just as faulty as those he had criticized. We have flawed proofs by Aghanis (5th century) and Simplicius (6th-century), two Byzantine scholars. Many others by medieval Islamic mathematicians have survived, including attempts by al-Jawhari and Thabit ibn Qurra in the 9th century, ...
... critical acumen, was just as faulty as those he had criticized. We have flawed proofs by Aghanis (5th century) and Simplicius (6th-century), two Byzantine scholars. Many others by medieval Islamic mathematicians have survived, including attempts by al-Jawhari and Thabit ibn Qurra in the 9th century, ...
Mathematics - Geometry
... User’s Guide to the Tennessee Mathematics Curriculum Framework. “Teachers move away from the stereotypical textbook-driven plan, which is linear in nature, and thus limited in efficiency, toward a plan which is spiraled and more in line with how human beings actually are wired to learn.” The Mathema ...
... User’s Guide to the Tennessee Mathematics Curriculum Framework. “Teachers move away from the stereotypical textbook-driven plan, which is linear in nature, and thus limited in efficiency, toward a plan which is spiraled and more in line with how human beings actually are wired to learn.” The Mathema ...
developing auxiliary resource materials
... exposed a limitation of Module 1 of the geometry curriculum. It needed more practice and assessment problems. A recent study by the Norwegian University of Science and Technology found that practice in mathematical tasks strengthen cognitive skills and results in a task being performed correctly upo ...
... exposed a limitation of Module 1 of the geometry curriculum. It needed more practice and assessment problems. A recent study by the Norwegian University of Science and Technology found that practice in mathematical tasks strengthen cognitive skills and results in a task being performed correctly upo ...
IMO problems from Kalva `s Web
... We use bold to denote vectors, so AB means the vector from A to B. We take some arbitrary origin and write the vector OA as A for short. Note that the vector to the midpoint of AB is (A + B)/2, so the vector from the midpoint of DE to the midpoint of AB is (A + B - D - E)/2. So the starting point is ...
... We use bold to denote vectors, so AB means the vector from A to B. We take some arbitrary origin and write the vector OA as A for short. Note that the vector to the midpoint of AB is (A + B)/2, so the vector from the midpoint of DE to the midpoint of AB is (A + B - D - E)/2. So the starting point is ...
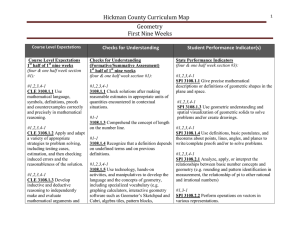
Geometry - Hickman County Schools
... 3108.4.21 Use properties of and theorems about parallel lines, perpendicular lines, and angles to prove basic theorems in Euclidean geometry (e.g., two lines parallel to a third line are parallel to each other, the perpendicular bisectors of line segments are the set of all points equidistant from t ...
... 3108.4.21 Use properties of and theorems about parallel lines, perpendicular lines, and angles to prove basic theorems in Euclidean geometry (e.g., two lines parallel to a third line are parallel to each other, the perpendicular bisectors of line segments are the set of all points equidistant from t ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.