Tangents and Secants to a Circle
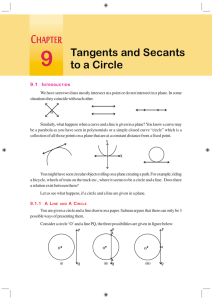
... How can you prove the converse of the above theorem. “If a line in the plane of a circle is perpendicular to the radius at its endpoint on the circle, then the line is tangent to the circle”. We can find some more results using the above theorem (i) Since there can be only one perpendicular OP at th ...
... How can you prove the converse of the above theorem. “If a line in the plane of a circle is perpendicular to the radius at its endpoint on the circle, then the line is tangent to the circle”. We can find some more results using the above theorem (i) Since there can be only one perpendicular OP at th ...
Plane Geometry - UVa-Wise
... With this preparatory discussion out of the way, it is time to begin examining the axioms we will use in this text. Our list is closely modeled on Hilbert’s list of axioms for plane geometry. Hilbert divided these axioms into several sets: the axioms of incidence, the axioms of order, the axioms of ...
... With this preparatory discussion out of the way, it is time to begin examining the axioms we will use in this text. Our list is closely modeled on Hilbert’s list of axioms for plane geometry. Hilbert divided these axioms into several sets: the axioms of incidence, the axioms of order, the axioms of ...
Geometry 2009 SOL
... • Use straight-edge tool to continue lines as far as possible • Parallel never can cross b crosses a and c d crosses all of them ...
... • Use straight-edge tool to continue lines as far as possible • Parallel never can cross b crosses a and c d crosses all of them ...
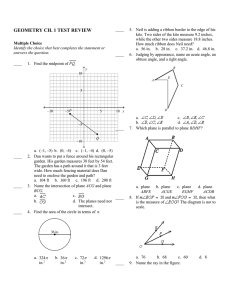
1Topic
... 6 The bisector of ]YXZ of ¢XYZ meets [YZ] at W. When a circle is drawn through X it touches [YZ] at W and cuts [XY] and [XZ] at P and Q respectively. Prove that ]YWP = ]ZWQ. 7 A, B and C are three points on a circle. The bisector of angle CAB cuts [BC] at P and the circle at Q. Prove that ]APC = ]AB ...
... 6 The bisector of ]YXZ of ¢XYZ meets [YZ] at W. When a circle is drawn through X it touches [YZ] at W and cuts [XY] and [XZ] at P and Q respectively. Prove that ]YWP = ]ZWQ. 7 A, B and C are three points on a circle. The bisector of angle CAB cuts [BC] at P and the circle at Q. Prove that ]APC = ]AB ...
Name: Ammie Hamilton S
... a. A dilation takes a line not passing through the center of the dilation to a parallel line, and leaves a line passing through the center unchanged. b. The dilation of a line segment is long ...
... a. A dilation takes a line not passing through the center of the dilation to a parallel line, and leaves a line passing through the center unchanged. b. The dilation of a line segment is long ...
Geometry and axiomatic Method
... real change on the structure of the system. Giving the undefined terms a specific meaning is called an interpretation of the axiom system. Suppose in the example of students and classes, we replace students and classes by points and lines respectively. Then, our axioms would be as follows: Axiom 1. ...
... real change on the structure of the system. Giving the undefined terms a specific meaning is called an interpretation of the axiom system. Suppose in the example of students and classes, we replace students and classes by points and lines respectively. Then, our axioms would be as follows: Axiom 1. ...
Curriculum Cluster 2
... Parallel and Perpendicular Lines a.1 Builds on knowledge of number, operation, and quantitative reasoning; patterns, and algebraic thinking, geometry, measurement, and probability and statistics, solve meaningful problems by representing and transforming figures and analyzing relationships. a.6 Make ...
... Parallel and Perpendicular Lines a.1 Builds on knowledge of number, operation, and quantitative reasoning; patterns, and algebraic thinking, geometry, measurement, and probability and statistics, solve meaningful problems by representing and transforming figures and analyzing relationships. a.6 Make ...
LSU College Readiness Program COURSE
... 3.6 Coordinate Geometry – The Slope of a Line (32) Find the slope of a line Interpret the slope-intercept form in an application Compare the slopes of parallel and perpendicular lines 3.7 Coordinate Geometry – Equations of Lines (26) Use the slope-intercept form Use the point-slope form Write the e ...
... 3.6 Coordinate Geometry – The Slope of a Line (32) Find the slope of a line Interpret the slope-intercept form in an application Compare the slopes of parallel and perpendicular lines 3.7 Coordinate Geometry – Equations of Lines (26) Use the slope-intercept form Use the point-slope form Write the e ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.