Chapter 9
... circular design, and sewed a blue ribbon on the circle that passes through the circle’s centre, O. She wants to sew on two more blue ribbons to the circle, as shown. a) What is the measure of the angle formed at the point on the circle where the two new ribbons meet? b) If the point where the new ri ...
... circular design, and sewed a blue ribbon on the circle that passes through the circle’s centre, O. She wants to sew on two more blue ribbons to the circle, as shown. a) What is the measure of the angle formed at the point on the circle where the two new ribbons meet? b) If the point where the new ri ...
Mathematics Syllabus Coverage - CBSE
... The CBSE-International is grateful for permission to reproduce and/or translate copyright material used in this publication. The acknowledgements have been included wherever appropriate and sources from where the material may be taken are duly mentioned. In case any thing has been missed out, the B ...
... The CBSE-International is grateful for permission to reproduce and/or translate copyright material used in this publication. The acknowledgements have been included wherever appropriate and sources from where the material may be taken are duly mentioned. In case any thing has been missed out, the B ...
2016 – 2017 - Huntsville City Schools
... similarity for triangles as the equality of all corresponding pairs of angles and the proportionality of all corresponding pairs of sides. (Alabama)Example 1: Image Given the two triangles above, show that they are similar. 4/8 = 6/12 They are similar by SSS. The scale factor is equivalent. Example ...
... similarity for triangles as the equality of all corresponding pairs of angles and the proportionality of all corresponding pairs of sides. (Alabama)Example 1: Image Given the two triangles above, show that they are similar. 4/8 = 6/12 They are similar by SSS. The scale factor is equivalent. Example ...
Geometry Overview
... triangle sum to 180°; base angles of isosceles triangles are congruent; the segment joining midpoints of two sides of a triangle is parallel to the third side and half the length; the medians of a triangle meet at a point. Use the definition of congruence in terms of rigid motions to show that two t ...
... triangle sum to 180°; base angles of isosceles triangles are congruent; the segment joining midpoints of two sides of a triangle is parallel to the third side and half the length; the medians of a triangle meet at a point. Use the definition of congruence in terms of rigid motions to show that two t ...
geometry - Swampscott High School
... The coordinates of the endpoints of ST and its image S'T' are given below. S (2, –4) T (–1, 1) S' (–2, –4) T' (1, 1) Which of the following single transformations maps ST to S'T' ? A. translation 4 units to the left B. rotation 180° clockwise about the origin C. reflection over the x-axis D. reflect ...
... The coordinates of the endpoints of ST and its image S'T' are given below. S (2, –4) T (–1, 1) S' (–2, –4) T' (1, 1) Which of the following single transformations maps ST to S'T' ? A. translation 4 units to the left B. rotation 180° clockwise about the origin C. reflection over the x-axis D. reflect ...
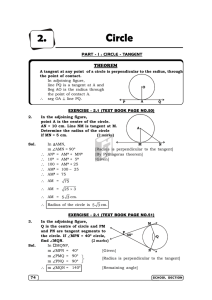
Circle - mt-iconnect.com
... But according to the given figure EK = 13 units. S C H O O L S E C TI O N ...
... But according to the given figure EK = 13 units. S C H O O L S E C TI O N ...
Study Guide
... line. A compass is any object that can be used to draw circles. The figures in Exercises 4–7 below were constructed using a straightedge. A figure can be traced if it has no more than two points where an odd number of segments meet. ...
... line. A compass is any object that can be used to draw circles. The figures in Exercises 4–7 below were constructed using a straightedge. A figure can be traced if it has no more than two points where an odd number of segments meet. ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.