An Introduction to Non-Euclidean Geometry
... 2. If equals are added to equals, then the wholes are equal. 3. If equals are subtracted from equals, then the remainders are equal. 4. Things which coincide with one another equal one another. 5. The whole is greater than the part. ...
... 2. If equals are added to equals, then the wholes are equal. 3. If equals are subtracted from equals, then the remainders are equal. 4. Things which coincide with one another equal one another. 5. The whole is greater than the part. ...
Geometry - Delaware Department of Education
... Cluster: Use coordinates to prove simple geometric theorems algebraically. .................. 49 9-11.G.GPE.4 – Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or ...
... Cluster: Use coordinates to prove simple geometric theorems algebraically. .................. 49 9-11.G.GPE.4 – Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or ...
Dividing a decimal by a whole number
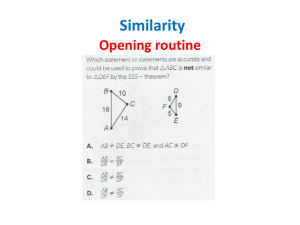
... Proportion: Is the name that is given to a statement that two ratios are equal. In a proportion the cross products are equal. Similar triangles: Triangles are similar when they preserve angle measures. Similar triangles: Corresponding side lengths in similar triangles are proportional. ...
... Proportion: Is the name that is given to a statement that two ratios are equal. In a proportion the cross products are equal. Similar triangles: Triangles are similar when they preserve angle measures. Similar triangles: Corresponding side lengths in similar triangles are proportional. ...
Euclid I-III
... Early mathematicians drew a distinction between an axiom and a postulate. Basically a postulate asserted that an object could be constructed while an axiom asserted a fact about an object. I have not drawn that distinction primarily because their view of geometry as an actual physically constructibl ...
... Early mathematicians drew a distinction between an axiom and a postulate. Basically a postulate asserted that an object could be constructed while an axiom asserted a fact about an object. I have not drawn that distinction primarily because their view of geometry as an actual physically constructibl ...
T. Sundara Row`s Geometric exercises in paper folding
... ope inclosing the first half. This latter process saved paper and had the obvious advantage of securing the post marks on the paper written upon. Paper-folding has been resorted to in teaching the Xlth Book of Euclid, which deals with figures of three dimensions.* ...
... ope inclosing the first half. This latter process saved paper and had the obvious advantage of securing the post marks on the paper written upon. Paper-folding has been resorted to in teaching the Xlth Book of Euclid, which deals with figures of three dimensions.* ...
What is Hyperbolic Geometry? - School of Mathematics, TIFR
... Department of Mathematics, RKM Vivekananda University. ...
... Department of Mathematics, RKM Vivekananda University. ...
The Project Gutenberg eBook #29807: Solid Geometry
... one plane can be passed. 67. Axiom 3. Two distinct planes cannot meet in one point only. 68. Determination of a Plane. A plane is said to be determined by certain elements (lines or points) if this plane contains these elements while no other plane does contain them. While two points determine a str ...
... one plane can be passed. 67. Axiom 3. Two distinct planes cannot meet in one point only. 68. Determination of a Plane. A plane is said to be determined by certain elements (lines or points) if this plane contains these elements while no other plane does contain them. While two points determine a str ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.