* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Arrangements and duality
Dessin d'enfant wikipedia , lookup
Cartesian coordinate system wikipedia , lookup
Conic section wikipedia , lookup
Steinitz's theorem wikipedia , lookup
Lie sphere geometry wikipedia , lookup
Euclidean geometry wikipedia , lookup
Rational trigonometry wikipedia , lookup
Perspective (graphical) wikipedia , lookup
Complex polytope wikipedia , lookup
Four color theorem wikipedia , lookup
Projective plane wikipedia , lookup
Duality (mathematics) wikipedia , lookup
CS 372: Computational Geometry
Lecture 13
Arrangements and Duality
Antoine Vigneron
King Abdullah University of Science and Technology
November 28, 2012
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
1 / 41
1
Introduction
2
Point-line duality
3
Upper envelopes
4
Arrangements of lines
5
An application of arrangements and duality
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
2 / 41
Outline
We saw planar graph duality in Lecture 10.
I
In this lecture, a different type of duality: point-line duality.
We introduce line arrangements.
These two notions can often be combined to solve apparently difficult
computational geometry problems.
References:
Textbook Chapter 8.
Dave Mount’s lecture notes, Lectures 8, 19 and 20.
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
3 / 41
Point-Line Duality
Point-Line Duality: A transformation that exchanges points and lines.
Motivation: For the same amount of work, twice as many results.
Theorem 1∗
Theorem 1
Duality
involves points and lines
involves lines and points
Program 1∗
Program 1
Duality
deals with points and lines
Antoine Vigneron (KAUST)
CS 372 Lecture 13
deals with lines and points
November 28, 2012
4 / 41
Point-Line Duality: Example
p(2, 1)
` : y = 2x − 1
(0.5, 0)
(0, −1)
notation:
p = `∗
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
5 / 41
Dual Point
Let ` be a non-vertical line.
I
` has equation ` : y = `a x − `b .
F
I
I
`a is the slope of `.
We associate the point `∗ = (`a , `b ) to `.
`∗ is called the dual of `.
We say that ` is a line in the primal plane.
Here, the primal plane is associated with a coordinate frame Oxy .
We say that `∗ is a point in the dual plane.
We will use a coordinate frame Uab for the dual plane.
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
6 / 41
Dual Point
y
b
`∗ (`a , `b )
`a
1
x
O
a
U
` : y = `a x − `b
(0, −`b )
Primal plane
Antoine Vigneron (KAUST)
Dual plane
CS 372 Lecture 13
November 28, 2012
7 / 41
Dual Line
Let p(px , py ) be a point in the primal plane.
Its dual is a line p ∗ in the dual plane with equation
p ∗ : b = px a − py .
y
b
p(px , py )
px
1
O
a
U
x
p ∗ : b = px a − py
(0, −py )
Primal plane
Antoine Vigneron (KAUST)
Dual plane
CS 372 Lecture 13
November 28, 2012
8 / 41
Self Inverse
Property (Self inverse)
For any point p in the primal plane, (p ∗ )∗ = p.
Proof:
p(px , py ) in the primal plane.
p ∗ : b = px a − py .
(p ∗ )∗ has coordinates (px , −(−py )).
Property (Self inverse)
For any line ` of the primal plane, (`∗ )∗ = `.
Proof:
` : y = `a x − `b .
`∗ (`a , `b ).
(`∗ )∗ : y = `a x − `b .
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
9 / 41
Point-Line Duality is Incidence Preserving
p∗
p
`∗
`
Primal plane
Antoine Vigneron (KAUST)
Dual plane
CS 372 Lecture 13
November 28, 2012
10 / 41
Point-Line Duality is Incidence Preserving
Property
p ∈ ` iff `∗ ∈ p ∗ .
Proof:
Assume p ∈ `.
I
I
I
It means py = `a px − `b .
So `b = px `a − py .
Thus (`a , `b ) ∈ p ∗ .
Now assume that `∗ ∈ p ∗ .
I
I
Then (p ∗ )∗ ∈ (`∗ )∗ .
By the self-inverse property, it yields p ∈ `.
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
11 / 41
Multiple Incidence
Corollary
p1 , p2 and p3 are collinear iff p1∗ , p2∗ and p3∗ intersect at a common point.
p3∗
p3
p2
p2∗
p1
p1∗
Primal plane
Antoine Vigneron (KAUST)
Dual plane
CS 372 Lecture 13
November 28, 2012
12 / 41
Order Reversing
Property (Order reversing)
p lies below ` iff p ∗ is above `∗ .
`
p∗
p
`∗
Primal plane
Antoine Vigneron (KAUST)
Dual plane
CS 372 Lecture 13
November 28, 2012
13 / 41
Example: Dual of a line segment
Let s = pq be a line segment in R2 .
How to define its dual?
Its dual s ∗ is the union of the duals of the points of s.
All the points in s are collinear, so all the lines in s ∗ pass through one
point.
So it is a double wedge. (See next slide.)
Property
A line ` intersect a segment s iff `∗ is in s ∗ .
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
14 / 41
Example: Dual of a line segment
p∗
s∗
`
q
`∗
s
p
q∗
Primal plane
Antoine Vigneron (KAUST)
Dual plane
CS 372 Lecture 13
November 28, 2012
15 / 41
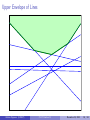
Upper Envelope of Lines
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
16 / 41
Upper Envelope of Lines
Definition (Upper envelope)
The upper envelope of a set of lines is the set of the points that are above
all lines.
How to compute the upper envelope of a set L of n lines?
Idea: use duality.
Lines configuration ⇒ points configuration.
We denote L∗ = {`∗ | ` ∈ L}.
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
17 / 41
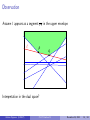
Observation
Assume ` appears as a segment pq in the upper envelope.
`
p
q
Interpretation in the dual space?
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
18 / 41
Observation
p and q are on or above all the lines in L.
So p ∗ and q ∗ are on or below all the points in L∗ .
L∗
p∗
q∗
Antoine Vigneron (KAUST)
`∗
CS 372 Lecture 13
November 28, 2012
19 / 41
Observation
So p ∗ and q ∗ are on the lower part of CH(L∗ ).
`∗ = p ∗ ∩ q ∗ is also on the lower part of CH(L∗ ).
We denote this lower part by LH(L∗ ).
CH(L∗ )
p∗
q∗
Antoine Vigneron (KAUST)
`∗
CS 372 Lecture 13
November 28, 2012
20 / 41
Consequences
The lines that appear in the upper envelope of L correspond to the points
that appear in the lower hull of L∗ . How to compute the upper envelope?
Compute the lower hull LH(L∗ ).
Traverse this chain from left to right, output the dual of the vertices.
This gives you a list of lines of L.
These are the lines that appear in the upper envelope.
They are in the same order as they appear in this upper envelope,
from left to right.
I
Why?
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
21 / 41
Consequences
We use the algorithm from Lecture 2.
It takes O(n log n) time.
So we can compute an upper envelope of lines in O(n log n) time.
So we can compute the intersection of n halfplanes in O(n log n)
time.
I
I
I
I
I
Split into two sets of halfplanes: those that go upward and those that
go downward.
The intersection of the upward halfplanes is an upper envelope of lines.
The other subset is a lower envelope. (Similar idea.)
Intersect these two chains. (Plane sweep for instance.)
Overall, it takes O(n log n) time.
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
22 / 41
Remarks
We have just seen that, in the plane, the following three problems are
equivalent:
I
I
I
Convex hull of a point set.
Upper (lower) envelope of lines.
Halfspace intersection.
In higher dimension, it is similar.
I
I
But the intersection of n half-spaces is a polytope that can have
Ω(nbd/2c ) vertices.
Voronoi diagrams and Delaunay triangulations can be seen as upper
envelopes in one dimension higher.
These problems, that are all related, are fundamental problems in
computational geometry.
RIC works well for these problems.
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
23 / 41
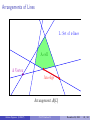
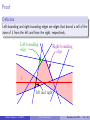
Arrangements of Lines
L: Set of n lines
A cell
A Vertex
An edge
Arrangement A(L)
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
24 / 41
Definition
Definition (Arrangement of lines)
Let L be a set of n lines in R2 . These lines subdivide R2 into several
regions, called cells. The edges of this subdivision are line segments or
half-lines. The vertices are intersection points between two lines of L. This
subdivision, with adjacency relation between vertices, edges and cells, is
called the arrangement A(L) of L.
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
25 / 41
Bounding Box
We restrict our attention to a bounding box B that contains all the
vertices of A(L).
B
Now all edges and faces are bounded.
How fast can we compute such a bounding box?
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
26 / 41
General Position Assumptions
No two lines are parallel.
No three lines intersect at one point.
A degenerate case:
- Two lines are parallel.
- Three lines intersect at one point.
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
27 / 41
Combinatorial Complexity
Definition (Combinatorial complexity)
The combinatorial complexity of an arrangement A(L) is the total number
of vertices, edges, and faces in A(L).
This quantity is Θ(n2 ) for an arrangement of n lines.
More precisely, if L is in general position.
I
I
I
A(L) has n2 vertices.
A(L) has n2edges.
A(L) has n2 + n + 1 faces.
Proof?
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
28 / 41
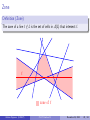
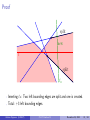
Zone
Definition (Zone)
The zone of a line ` ∈
/ L is the set of cells in A(L) that intersect `.
`
zone of `
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
29 / 41
Zone Theorem
Theorem (Zone Theorem)
The total number of edges of all the cells in the zone of a line ` ∈
/ L in
A(L) is O(n).
In other words: the combinatorial complexity of the zone of a line is
linear.
Why is it not obvious?
Some lines of L appear in several cells of the zone; See previous slide.
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
30 / 41
Proof
Definition
Left-bounding and right-bounding edges are edges that bound a cell of the
zone of L from the left and from the right, respectively.
Left-bounding
edge
Right-bounding
edge
`
left and right
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
31 / 41
Proof
We insert lines of L from left to right along `.
Inserting a line increases by at most 3 the number of left bounding
edges.
It follows that the zone has at most 3n left bounding edges.
So the zone of ` has at most 6n edges.
See picture next slide, and detailed proof in D. Mount’s notes.
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
32 / 41
Proof
split
new
`
split
`n
Inserting `n : Two left bounding edges are split and one is created.
Total: +3 left bounding edges.
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
33 / 41
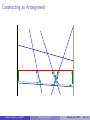
Constructing an Arrangement
`
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
34 / 41
Constructing an arrangement
Incremental algorithm.
We insert the lines one by one and update the arrangement.
Arrangement maintained in a Doubly Connected Edge List.
Insertion of a new line `.
Find the leftmost point of ` in the bounding box and the cell that
contains it.
It takes O(n) time.
Traverse the zone of ` from left to right and update the arrangement
accordingly.
By the Zone Theorem, can be done in O(n) time.
Overall, we compute a DCEL of A(L) in O(n2 ) time.
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
35 / 41
An application of arrangements and duality
Problem (Smallest triangle)
Given a set P of n points in R2 , find the triangle with smallest area whose
vertices are in P.
We assume general position: No three points are collinear.
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
36 / 41
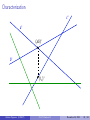
Characterization
Let (a, b) ∈ P 2
How can we find c ∈ P such that area of a, b, c is minimized?
Find the largest empty corridor along line ab.
`c
a
b
c
c lies on its boundary.
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
37 / 41
Characterization
c lies on a line `c such that:
`c is parallel to ab,
and there is no other line with same slope between ab and `c .
What does it mean in the dual plane?
We call (ab)∗ the dual of line ab.
(`c )∗ is on c ∗ .
(`c )∗ and (ab)∗ have same abscissa.
No line p ∗ where p ∈ P crosses the line segment with endpoints (ab)∗
and (`c )∗ .
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
38 / 41
Characterization
c∗
a∗
(ab)∗
b∗
(`c )∗
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
39 / 41
Consequences
(`c )∗ is in the same cell of A(P ∗ ) as (ab)∗ .
(`c )∗ is vertically above or below (ab)∗ .
Once A(P ∗ ) is computed, only two candidates involving a and b.
We compute A(P ∗ ) in O(n2 ) time.
For all cell of this arrangement, we compute by plane sweep the point
of the boundary that is vertically above or below every vertex of the
cell.
It takes time linear in the number of edges of the cell as they are
given in counterclockwise order.
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
40 / 41
Algorithm
For each triple a∗ , b ∗ , c ∗ we found, we can compute the area of
triangle a, b, c in O(1) time.
We maintain the minimum value found so far in O(1) time by triangle
we consider.
Overall, the running time of our algorithm is proportional to the
combinatorial complexity of A(P ∗ ).
So it runs in O(n2 ) time.
Antoine Vigneron (KAUST)
CS 372 Lecture 13
November 28, 2012
41 / 41