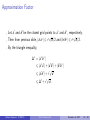Download CS 372: Computational Geometry Lecture 14 Geometric

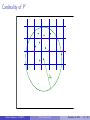
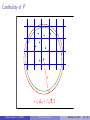
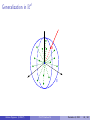
CS 372: Computational Geometry
Lecture 14
Geometric Approximation Algorithms
Antoine Vigneron
King Abdullah University of Science and Technology
December 5, 2012
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
1 / 46
1
Introduction
2
The diameter problem
3
A 2-approximation algorithm
4
Approximation scheme
5
Rounding to a grid
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
2 / 46
Outline
Introduction to geometric approximation algorithms.
Example: Computing the diameter of a point-set.
Simple 2-approximation algorithm.
Two approaches for ε-approximation:
I
I
Rounding.
Projection.
References:
Sariel Har Peled’s book.
Paper by T. Chan, Approximating the diameter, width, smallest
enclosing cylinder, and minimum-width annulus, Section 2.
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
3 / 46
The Diameter Problem
P
Input: a set P of n points in Rd .
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
4 / 46
The Diameter Problem
a∗
P
∆∗ = |a∗ b ∗ |
b∗
Input: a set P of n points in Rd .
Output: the maximum distance ∆∗ between any two points of P.
∆∗ is called the diameter of P.
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
5 / 46
Brute Force Algorithm
Computing the distance between two points:
If a = (a1 , a2 , . . . , ad ) and b = (b1 , b2 , . . . , bd ), then
q
|ab| = (b1 − a1 )2 + (b2 − a2 )2 + · · · + (bd − ad )2 .
It takes O(d) time.
Here we assume that d is constant: d = O(1).
I
We are in fixed dimension.
Then we can compute |ab| in O(1) time.
Computing the diameter:
Brute force: Check all pairs in P 2 and keep the maximum distance.
Brute force takes O(n2 ) time.
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
6 / 46
Approximation Algorithms
Definition (c-factor approximation)
We say that ∆ is a c-factor approximation to ∆∗ if ∆ 6 ∆∗ 6 c∆.
Definition (c-approximation algorithm)
A c-approximation algorithm for a maximization problem is an algorithm
that computes a c-factor approximation of the optimum in polynomial
time.
We will give a 2-approximation algorithm for the diameter problem.
That is, we find ∆0 such that ∆0 6 ∆∗ 6 2∆0
O(n) time, very simple.
Best known exact algorithms are slower and complicated.
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
7 / 46
2-Approximation Algorithm
P
a
Pick a point a ∈ P.
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
8 / 46
2-Approximation Algorithm
P
b
a
Pick a point a ∈ P.
Find b such that |ab| is maximum.
∆0 = |ab|.
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
9 / 46
Analysis
Pick any point a ∈ P.
I
O(1) time.
Find b ∈ P such that |ab| is maximum.
I
I
Just go through the list of points in P and keep the maximum distance
to a.
It takes O(n) time.
Conclusion: This algorithm runs in O(n) time.
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
10 / 46
Proof of Correctness
We need to prove that ∆0 is a 2-factor approximation. of ∆∗ .
It means ∆0 6 ∆∗ 6 2∆0 .
Since (a, b) ∈ P 2 , clearly, ∆0 = |ab| 6 ∆∗ .
We also need to prove that ∆∗ 6 2∆0 .
I
I
I
Let a∗ and b ∗ denote two points such that |a∗ b ∗ | = ∆∗ .
By definition of b we have |aa∗ | 6 |ab| and |ab ∗ | 6 |ab|.
By the triangle inequality
∆∗ = |a∗ b ∗ |
6 |a∗ a| + |ab ∗ |
6 |ab| + |ab|
= 2∆0 .
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
11 / 46
Concluding Remark
The running time is optimal.
If we do not assume d = O(1):
I
I
I
This algorithm still works.
But the running time has to be written O(dn).
It is still optimal as we need Θ(nd) time to read the input.
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
12 / 46
(1 + ε)-Approximation Algorithms
We just found a 2-approximation algorithm.
We would like to obtain a better approximation.
Let ε > 0 be a real number.
I
I
In this lecture, we assume ε < 1.
ε should be thought of as being small, say ε = 0.1 or ε = 0.01.
We want to design a (1 + ε)-approximation algorithm.
The result will be ∆ such that ∆ 6 ∆∗ 6 (1 + ε)∆.
I
I
In other words, the relative error we allow is ε.
So ε = 0.01 means a 1% error.
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
13 / 46
Analysis
How to analyze a (1 + ε)-approximation algorithm?
The running time is expressed as a function of n and ε using O(·)
notation.
I
For instance, the last algorithm in this lecture runs in time.
3
O n + (1/ε) 2 (d−1)
I
Since d = 0(1), it is polynomial in n and 1/ε.
F
It is an FPTAS (Fully Polynomial Time Approximation Scheme).
The running time is linear in n.
Problem: exponential in d.
I
These algorithms are only interesting in low dimension d.
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
14 / 46
Idea
Start with a set P of n points.
Transform it into a set P 0 such that:
I
I
The cardinality |P 0 | is small.
The diameter ∆0 of P 0 is a good approximation of ∆.
Then find ∆0 by brute force
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
15 / 46
Rounding to a Grid
P
0
0
Consider a regular grid over Rd .
The side length of the grid is 0 , to be specified later.
Intuition: we will choose 0 ' ∆∗ , it is the error we allow.
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
16 / 46
Rounding to a Grid
P
Replace each point of P with the nearest grid point.
This operation is called rounding.
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
17 / 46
Rounding to a Grid
P0
The grid points we obtain form the set P 0 .
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
18 / 46
Rounding to a Grid
c0
∆0
d0
P0
Compute the diameter ∆0 of P 0 by brute force.
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
19 / 46
Intuition
P 0 is a d-dimensional point set with diameter ∆0 .
The points are on a grid with side length 0 ; we will choose it such
that 0 ' ∆0 .
So in the worst case, there are about as many points in P 0 as in a
(1/) × (1/) · · · × (1/) grid in Rd .
There are O((1/)d ) such points.
We can compute ∆0 by brute force in time O((1/)2d ).
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
20 / 46
How to Perform Rounding?
The grid points have coordinates (k1 0 , k2 0 , . . . kd 0 ) where each ki is
an integer.
Let p = (p1 , p2 , . . . pd ) ∈ P.
How can we find the closest grid point p 0 ?
We need to find the closest integer ki to pi /0 .
It is given by the formula
pi
1
ki = 0 +
.
2
p is rounded to p 0 = (k1 0 , k2 0 , . . . kd 0 ).
It takes O(d) = O(1) time.
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
21 / 46
Rounding Error
Property
√
Let x ∈ Rd , and let x 0 be the closest grid point to x. Then |xx 0 | 6 0 d/2.
Proof: Apply previous slide formula.
Intuition:
I
x is in a hypercube centered at x 0 with side length 0 .
√
0 d
x0
x
0
I
0
√
This hypercube diagonal has length 0 d.
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
22 / 46
Approximation Factor
Let a0 and b 0 be the closest grid points to a∗ and b ∗ , respectively.
√
√
Then from previous slide, |a0 a∗ | 6 0 d/2 and |b 0 b ∗ | 6 0 d/2.
By the triangle inequality,
∆∗ = |a∗ b ∗ |
6 |a∗ a0 | + |a0 b 0 | + |b 0 b ∗ |
√
6 |a0 b 0 | + 0 d
√
6 ∆0 + 0 d.
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
23 / 46
Approximation Factor
Let c 0 and d 0 be two points of P 0 such that |c 0 d 0 | = ∆0 .
Let c and d be points of P that have been rounded to c 0 and d 0 ,
respectively.
√
√
Then |cc 0 | 6 0 d/2 and |dd 0 | 6 0 d/2.
So by the triangle inequality,
∆0 = |c 0 d 0 |
√
6 |cd| + 0 d.
Of course |cd| 6 ∆∗ .
It follows that
Antoine Vigneron (KAUST)
√
∆0 6 ∆∗ + 0 d
CS 372 Lecture 14
December 5, 2012
24 / 46
Approximation Factor
We obtained
√
√
∆0 − 0 d 6 ∆∗ 6 ∆0 + 0 d.
√
We choose ∆ = ∆0 − 0 d, so
√
∆ 6 ∆∗ 6 ∆ + 20 d.
√
We want to make sure that 20 d 6 ∆∗ /2.
√
Since ∆0 6 ∆∗ , it suffices that 20 d 6 ∆0 /2.
√
So we first compute ∆0 , and then we set 0 = ∆0 /(4 d).
It follows that ∆ 6 ∆∗ 6 ∆ + ∆∗ /2.
Problem: We wanted to show that ∆ 6 ∆∗ 6 ∆ + ∆.
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
25 / 46
Technical Difficulty
Intuition: The relative error is less than , so it is OK.
Proof: We want to prove that ∆∗ 6 ∆ + ∆.
I
I
We know that ∆∗ 6 ∆ + ∆∗ /2.
Then
1
∆
1 − /2
2
3
= 1+ +
+
+ . . . ∆.
2
4
8
∆∗ 6
I
Since < 1, we get
1
1 1 1
∆ 6 1+
+ + +
...
∆
2 4 8 16
∗
= (1 + )∆.
So ∆ is a (1 + )-factor approximation of ∆∗ .
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
26 / 46
Cardinality of P 0
∆0
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
27 / 46
Cardinality of P 0
r
√
r 6 ∆0 + 0 d/2
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
28 / 46
Cardinality of P 0
r0
B
√
r 0 6 ∆0 + 0 d/2 + 0 /2
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
29 / 46
Cardinality of P 0
All the points of P are in a sphere with radius ∆0 .
√
So all the points of P 0 are in a sphere with radius ∆0 + 0 d/2.
To each point p ∈ P 0 , we associate a ball b(p) centered at p with
radius 0 /2.
These balls
√ are disjoint and contained in a ball B with radius
∆0 + 0 ( d/2 + 1/2) 6 2∆0 .
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
30 / 46
How Many Grid Points are There?
The volume of a ball with radius r in dimension d is Cd r d , where Cd
depends only on d.
So the number of balls b(p), p ∈ P 0 is at most
16√d d
Cd (2∆0 )d
= O((1/)d ).
=
Cd (0 /2)d
Each point p ∈ P 0 is in exactly one ball b(p).
So |P 0 | = O((1/)d ).
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
31 / 46
Summary
Compute ∆0 in O(n) time.
√
Round all the points to a grid with side length 0 = ∆0 /(4 d).
I
I
I
It takes O(n) time.
There are O((1/)d ) such points.
We denote by P 0 the set of rounded points.
Compute the diameter ∆0 of P 0 by brute force.
I
It takes O((1/)2d ) time.
√
∆0 − 0 d is a (1 + )-factor approximation of the diameter ∆∗ of P.
Running time: O(n + (1/)2d ).
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
32 / 46
Grid Cleaning: Example in R2
b̂
â
P0
â is the lowest point on a vertical line
b̂ is the highest point on a vertical line
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
33 / 46
Grid Cleaning: Example in R2
b̂
â
P0
Idea: keep only the highest and the lowest point on each vertical line.
Then run the brute-force algorithm.
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
34 / 46
Analysis in R2
Only O(1/) points remain after grid cleaning.
So the algorithm runs in O(n + (1/)2 ) time.
In higher dimension, same idea.
I
I
I
I
Consider all the points that coincide in their first (d − 1) coordinates.
Keep only highest and lowest.
Then only O((1/)d−1 ) remain from P 0 .
So rounding + grid cleaning yields a running time O(n + (1/)2d−2 ).
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
35 / 46
Projecting on Lines
We measure angles in radian.
That is, an angle is in [0, 2π].
Property
For any α,
1−
α2
6 cos α 6 1.
2
Idea: We get a relative error ε by choosing α to be roughly
Antoine Vigneron (KAUST)
CS 372 Lecture 14
√
ε.
December 5, 2012
36 / 46
Projecting on Lines
√
b
a
b0
`
a0
|a0 b 0 | 6 |ab| 6 (1 + ε)|a0 b 0 |
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
37 / 46
Projecting on Lines
Assume that the angle between line ab and line ` is at most
a0
(resp.
b0 )
√
.
is the orthogonal projection of a (resp. b) into `.
Then
|a0 b 0 | 6 |ab|
1
1 − /2
2 8
0 0
+
+ ... .
= |a b | × 1 + +
2
4
8
6 |a0 b 0 | ×
Since we assume that < 1, we obtain
|a0 b 0 | 6 |ab| 6 |a0 b 0 |(1 + ).
In other words, |a0 b 0 | is a (1 + )–factor approximation of |ab|.
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
38 / 46
Idea
P` obtained by projecting P onto a line `.
a∗
P
`
b∗
P`
Compute the diameter of P` .
I
Can be done in O(n) time: Find maximum and minimum along `.
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
39 / 46
Idea
√
If the angle between ` and a∗ b ∗ is less than , then the diameter of
P` is a (1 + )-factor approximation of ∆∗ .
√
How can we find a line that makes an angle with ab?
I
I
Pick several lines.
√
√
In the plane: Pick direction k for each k ∈ [0, π/ ].
√
O( ) cones
√
with angular diameter Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
40 / 46
Algorithm in R2
√
For any integer k ∈ [0, π/ ], we denote by `k a line that makes
√
angle k with horizontal.
`k
√
k ε
Project P onto `k , obtaining P`k .
The maximum of the diameter of P`k over all k is a (1 + )-factor
approximation of the diameter or P.
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
41 / 46
Algorithm in R2 : Analysis
Projecting onto a particular `k takes O(n) time.
Computing the diameter of P`k takes O(n) time.
√
There are O(1/ ) such lines.
√
Overall running time O(n/ ).
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
42 / 46
Algorithm in R2 : Proof
Let θ be the angle of a∗ b ∗ with horizontal.
√
√
There exists k such that k 6 θ < (k + 1) .
√
The angle between a∗ b ∗ and `k is at most .
So the diameter of P`k is at least ∆∗ /(1 + ).
So the output of the algorithm is at least ∆∗ /(1 + ).
On the other hand, the algorithm only looks at distances between two
projected points, which are always smaller than ∆∗ .
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
43 / 46
Generalization in Rd
d
S
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
44 / 46
Generalization in Rd
Problem: Find a set of directions that approximates well the whole
set of directions.
Reformulation:
I
I
I
I
Let S be the unit sphere in Rd .
Find D ⊂ S with small cardinality such that
√
∀x ∈ S there is a point d ∈ D such that |dx| 6 .
A point d ∈ D is associated with the line through√
the origin and d.
d handles a cone of direction with angular radius .
Such a set D with cardinality O((1/)(d−1)/2 ) can be computed
efficiently.
So the algorithm runs in time O(n(1/)(d−1)/2 ).
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
45 / 46
Combining the two Techniques
Running times:
I
I
Grid + cleaning: O(n + (1/)2d−2 ).
Projections: O(n(1/)(d−1)/2 ).
Approach:
I
I
I
I
I
First round to P 0 and do grid cleaning.
We are left with O((1/)d−1 ) points.
Project on lines.
Overall running time: O(n + (1/)3(d−1)/2 )
Technical problem: the approximation factor is now about 1 + 2. (how
to solve it?)
Antoine Vigneron (KAUST)
CS 372 Lecture 14
December 5, 2012
46 / 46