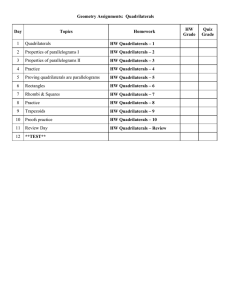
Assignments Quadrilaterals
... 3. In parallelogram ABCD, mA = 2x + 20 and mB = 4x – 50. Find the value of x and determine whether ABCD is a rectangle. Give a reason. 4. In rectangle ABCD, the diagonals AC and BD intersect at E. If AE = 3x + y, BE = 4x – 2y, CE = 20, find the values of x and y. 5. Which of the following is not s ...
... 3. In parallelogram ABCD, mA = 2x + 20 and mB = 4x – 50. Find the value of x and determine whether ABCD is a rectangle. Give a reason. 4. In rectangle ABCD, the diagonals AC and BD intersect at E. If AE = 3x + y, BE = 4x – 2y, CE = 20, find the values of x and y. 5. Which of the following is not s ...
Geometry - Hickman County Schools
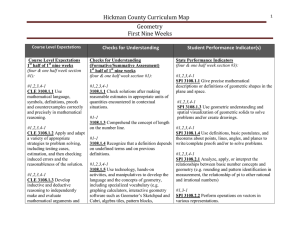
... 3108.4.21 Use properties of and theorems about parallel lines, perpendicular lines, and angles to prove basic theorems in Euclidean geometry (e.g., two lines parallel to a third line are parallel to each other, the perpendicular bisectors of line segments are the set of all points equidistant from t ...
... 3108.4.21 Use properties of and theorems about parallel lines, perpendicular lines, and angles to prove basic theorems in Euclidean geometry (e.g., two lines parallel to a third line are parallel to each other, the perpendicular bisectors of line segments are the set of all points equidistant from t ...
Geometry and axiomatic Method
... B. C. He insisted that, geometric statements must be established by deductive reasoning rather than by trial and error. He was familiar with the computations recorded from Egyptian and Babylonian mathematics, and he developed his logical geometry by determining which results were correct. The next m ...
... B. C. He insisted that, geometric statements must be established by deductive reasoning rather than by trial and error. He was familiar with the computations recorded from Egyptian and Babylonian mathematics, and he developed his logical geometry by determining which results were correct. The next m ...
Document
... 2. All even numbers are divisible by 2. 3. Determine if the statement “If n2 = 144, then n = 12” is true. If false, give a counterexample. ...
... 2. All even numbers are divisible by 2. 3. Determine if the statement “If n2 = 144, then n = 12” is true. If false, give a counterexample. ...
From Hilbert to Tarski - HAL
... First, we had to change the lower dimensional axiom. Hilbert states that there exists three non collinear points and three points are said to be collinear if there exists a line going through these three points. This assumption is not enough, because in a world without lines, assuming that there are ...
... First, we had to change the lower dimensional axiom. Hilbert states that there exists three non collinear points and three points are said to be collinear if there exists a line going through these three points. This assumption is not enough, because in a world without lines, assuming that there are ...
Geometry - Eleanor Roosevelt High School
... Let k represent “Kurt plays baseball.” Let a represent “Alicia plays baseball.” Let n represent “Nathan plays soccer.” Write each given sentence in symbolic form: a.Alicia plays baseball or Alicia does not play baseball (a V ~a) b.It is not true that Kurt or Alicia play baseball (~(k V a)) Mr. Chin- ...
... Let k represent “Kurt plays baseball.” Let a represent “Alicia plays baseball.” Let n represent “Nathan plays soccer.” Write each given sentence in symbolic form: a.Alicia plays baseball or Alicia does not play baseball (a V ~a) b.It is not true that Kurt or Alicia play baseball (~(k V a)) Mr. Chin- ...
Geometry - Eleanor Roosevelt High School
... An indirect proof works because the negation of the statement to be proved is false, then we can conclude that the statement is true ...
... An indirect proof works because the negation of the statement to be proved is false, then we can conclude that the statement is true ...
Contemporary Arguments For A Geometry of Visual Experience
... awareness of the shape and location of objects at a distance. However, it would be unwarranted to infer from this alone that what it is like to see by means of sonar is the same as what it is like to see by means of eyes. For example, the geometry could be different, even though the topology is not, ...
... awareness of the shape and location of objects at a distance. However, it would be unwarranted to infer from this alone that what it is like to see by means of sonar is the same as what it is like to see by means of eyes. For example, the geometry could be different, even though the topology is not, ...
Proving that a Quadrilateral is a Parallelogram Any of the methods
... Name Honors Geometry Given: CirCle H and CirCle "Prove: HELO is a parallelogram ...
... Name Honors Geometry Given: CirCle H and CirCle "Prove: HELO is a parallelogram ...