Geometry - Prescott Unified School District
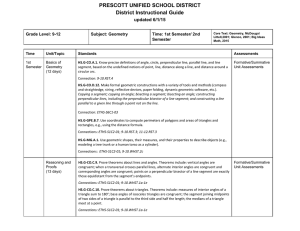
... Use coordinates to prove simple geometric theorems algebraically . For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on the circle centered at the origin and containing the point (0, 2). Co ...
... Use coordinates to prove simple geometric theorems algebraically . For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on the circle centered at the origin and containing the point (0, 2). Co ...
Given: Parallelogram ABCD with diagonal
... Theorem: If two angles are supplementary and one is a right angle, then Given: A supplementary to B; A is a right angle Prove: B is a right angle ...
... Theorem: If two angles are supplementary and one is a right angle, then Given: A supplementary to B; A is a right angle Prove: B is a right angle ...
2 - Ohio State Department of Mathematics
... the nonorientable S1 –bundle over P instead of P × S1 , where w1 of the associated vector bundle is w1 (P). The total space E of the S1 –bundle is then a 6–dimensional, orientable, polyhedral homology manifold with boundary. The restriction of the S1 – bundle to ∂P5 is orientable so ∂E = ∂P5 × S1 re ...
... the nonorientable S1 –bundle over P instead of P × S1 , where w1 of the associated vector bundle is w1 (P). The total space E of the S1 –bundle is then a 6–dimensional, orientable, polyhedral homology manifold with boundary. The restriction of the S1 – bundle to ∂P5 is orientable so ∂E = ∂P5 × S1 re ...
2-1
... Check It Out! Example 3 Make a conjecture about the lengths of male and female whales based on the data. Average Whale Lengths Length of Female (ft) ...
... Check It Out! Example 3 Make a conjecture about the lengths of male and female whales based on the data. Average Whale Lengths Length of Female (ft) ...
Geometer`s Sketchpad and the New Geometry Strands
... Instructions Sample Activities Key Curriculum Press (some are free) Mathbits Library of Resources from the Math Forum ...
... Instructions Sample Activities Key Curriculum Press (some are free) Mathbits Library of Resources from the Math Forum ...