Mapping for Instruction - First Nine Weeks
... The Mapping for Instruction has been set up according to each SOL that is taught in the specific 9-weeks. Note that only part of some SOLs may be taught in a certain 9-weeks. Each student should have a graphing calculator for use throughout this course. The instructor should use the calculator for i ...
... The Mapping for Instruction has been set up according to each SOL that is taught in the specific 9-weeks. Note that only part of some SOLs may be taught in a certain 9-weeks. Each student should have a graphing calculator for use throughout this course. The instructor should use the calculator for i ...
Geometry - Pearson
... This document demonstrates how Pearson’s High School Series by Elayn Martin-Gay, ©2016, meets the standards of the Common Core State Standards for Mathematics, PARRC Model Content Frameworks Mathematics - Algebra I. Pearson’s High School Series by Elayn Martin-Gay, ©2016, consists of three fully-dig ...
... This document demonstrates how Pearson’s High School Series by Elayn Martin-Gay, ©2016, meets the standards of the Common Core State Standards for Mathematics, PARRC Model Content Frameworks Mathematics - Algebra I. Pearson’s High School Series by Elayn Martin-Gay, ©2016, consists of three fully-dig ...
QUOTIENTS IN ALGEBRAIC AND SYMPLECTIC GEOMETRY 1
... is proper, then X/G is Hausdorff: given two distinct orbits G · x1 and G · x2 as (x1 , x2 ) is not in the image of Γ (which is closed in X × X) there is an open neighbourhood U1 × U2 ⊂ X × X of (x1 , x2 ) preserved by G which is disjoint from the image of Γ and π(U1 ) and π(U2 ) are disjoint open ne ...
... is proper, then X/G is Hausdorff: given two distinct orbits G · x1 and G · x2 as (x1 , x2 ) is not in the image of Γ (which is closed in X × X) there is an open neighbourhood U1 × U2 ⊂ X × X of (x1 , x2 ) preserved by G which is disjoint from the image of Γ and π(U1 ) and π(U2 ) are disjoint open ne ...
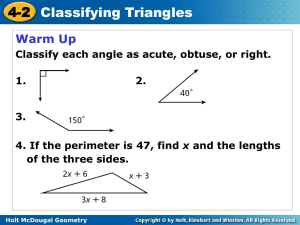
Geo 2.1 Using Inductive Reasoning to Make Conjectures
... Using Inductive Reasoning to 2-1 Make Conjectures When several examples form a pattern and you assume the pattern will continue, you are applying inductive reasoning. Inductive reasoning is the process of reasoning that a rule or statement is true because specific cases are true. You may use induct ...
... Using Inductive Reasoning to 2-1 Make Conjectures When several examples form a pattern and you assume the pattern will continue, you are applying inductive reasoning. Inductive reasoning is the process of reasoning that a rule or statement is true because specific cases are true. You may use induct ...
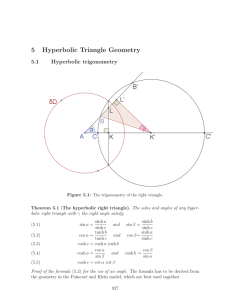
5 Hyperbolic Triangle Geometry
... ”The genuine hyperbolic case” The three bisectors are all divergently parallel to each other. There exists a line l perpendicular to all three bisectors. All three vertices have the same distance from line l. Hence there exists an equidistance line through the three vertices of the triangle. ”The bo ...
... ”The genuine hyperbolic case” The three bisectors are all divergently parallel to each other. There exists a line l perpendicular to all three bisectors. All three vertices have the same distance from line l. Hence there exists an equidistance line through the three vertices of the triangle. ”The bo ...
1 Hyperbolic Geometry The fact that an essay on geometry such as
... they can be derived from just the first four postulates. The reader may refer to these at their leisure in the appendix at the end of this paper. Certain fundamental axioms of order, continuity, and congruence will also be assumed as valid for our discourse. One such axiom of order which will come u ...
... they can be derived from just the first four postulates. The reader may refer to these at their leisure in the appendix at the end of this paper. Certain fundamental axioms of order, continuity, and congruence will also be assumed as valid for our discourse. One such axiom of order which will come u ...