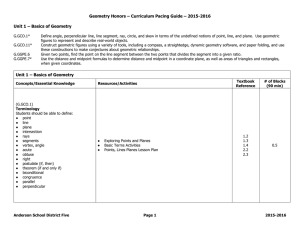
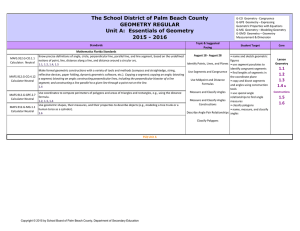
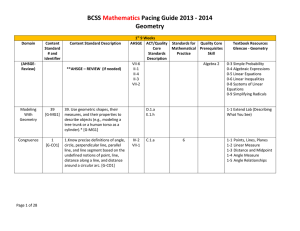
Geometry Honors – Curriculum Pacing Guide – 2015
... Represent translations, reflections, rotations, and dilations of objects in the plane by using paper folding, sketches, coordinates, function notation, and dynamic geometry software, and use various representations to help understand the effects of simple transformations and their compositions. Desc ...
... Represent translations, reflections, rotations, and dilations of objects in the plane by using paper folding, sketches, coordinates, function notation, and dynamic geometry software, and use various representations to help understand the effects of simple transformations and their compositions. Desc ...
Fundamentals of Algebra, G t d Geometry, and Trigonometry
... Integer – integers are numbers that are positive, negative, or zero and can be written without a fractional or decimal component. (Examples: -2, -1, 0, 1, 2, 65, and -756 are integers; 1.6, 1½, -2.4, and -5/6 are not integers.) A fraction is a number that can represent part of a whole. The top numbe ...
... Integer – integers are numbers that are positive, negative, or zero and can be written without a fractional or decimal component. (Examples: -2, -1, 0, 1, 2, 65, and -756 are integers; 1.6, 1½, -2.4, and -5/6 are not integers.) A fraction is a number that can represent part of a whole. The top numbe ...
is a parallelogram. - Plainfield Public Schools
... parallelogram. Now you will be given the properties of a quadrilateral and will have to tell if the quadrilateral is a parallelogram. To do this, you can use the definition of a parallelogram or the conditions below. ...
... parallelogram. Now you will be given the properties of a quadrilateral and will have to tell if the quadrilateral is a parallelogram. To do this, you can use the definition of a parallelogram or the conditions below. ...
The School District of Palm Beach County GEOMETRY REGULAR
... Represent transformations in the plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not (e.g., translation v ...
... Represent transformations in the plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not (e.g., translation v ...