Name: Period: ______ Geometry Unit 3: Parallel and Perpendicular
... REVIEW: Answer always, sometimes, or never for each question. 1. A scalene triangle is regular. 2. A theorem is a proven conjecture. 3. Planes intersect in a point. 4. Space is an infinite number of points. 5. A line can be named using three points. 6. Two points are collinear. 7. Two lines w ...
... REVIEW: Answer always, sometimes, or never for each question. 1. A scalene triangle is regular. 2. A theorem is a proven conjecture. 3. Planes intersect in a point. 4. Space is an infinite number of points. 5. A line can be named using three points. 6. Two points are collinear. 7. Two lines w ...
john f. kennedy high school geometry course syllabus
... Prove the Pythagorean theorem. Use the Pythagorean theorem to determine distance and find missing lengths of sides in right triangles. Perform basic constructions with a straightedge and compass, such as angle bisectors, perpendicular bisectors, and the line parallel to a given line through a point ...
... Prove the Pythagorean theorem. Use the Pythagorean theorem to determine distance and find missing lengths of sides in right triangles. Perform basic constructions with a straightedge and compass, such as angle bisectors, perpendicular bisectors, and the line parallel to a given line through a point ...
Geometry A Course
... successfully complete Geometry A and Geometry B will meet the Geometry requirement for graduation. This course will help students develop communication skills, enhance reasoning, and make connections within mathematics to other disciplines and the real world. In this course, students are engaged in ...
... successfully complete Geometry A and Geometry B will meet the Geometry requirement for graduation. This course will help students develop communication skills, enhance reasoning, and make connections within mathematics to other disciplines and the real world. In this course, students are engaged in ...
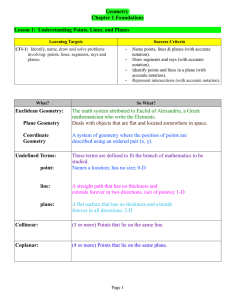
Day 2 notes and assignment
... Exploring Parallel Lines Intro Activity Transversal – a line that intersects two or more other lines at distinct points. ...
... Exploring Parallel Lines Intro Activity Transversal – a line that intersects two or more other lines at distinct points. ...
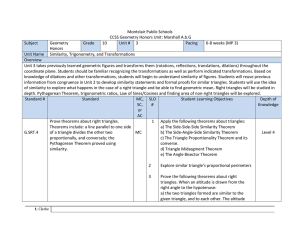
Geometry 3rd Nine Weeks Pacing Guide Summary
... 33. [G-GPE.7] Use coordinates to compute perimeters of polygons and areas of triangles and rectangles, e.g., using the distance formula.* 17. [G-SRT.4] Prove theorems about triangles. Theorems include a line parallel to one side of a triangle divides the other two proportionally, and conversely; the ...
... 33. [G-GPE.7] Use coordinates to compute perimeters of polygons and areas of triangles and rectangles, e.g., using the distance formula.* 17. [G-SRT.4] Prove theorems about triangles. Theorems include a line parallel to one side of a triangle divides the other two proportionally, and conversely; the ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.