http://www.ms.uky.edu/~droyster/courses/spring04/classnotes/Chapter%2009.pdf
... −M followed by inversion in the unit circle. This map ϕ is an isometry because it is the composition of two isometries. Note that M is first sent to O and then to ∞ by inversion. Thus, the image of Γ is a (Euclidean) line. Since the center of the circle is on the real axis, the circle intersects the ...
... −M followed by inversion in the unit circle. This map ϕ is an isometry because it is the composition of two isometries. Note that M is first sent to O and then to ∞ by inversion. Thus, the image of Γ is a (Euclidean) line. Since the center of the circle is on the real axis, the circle intersects the ...
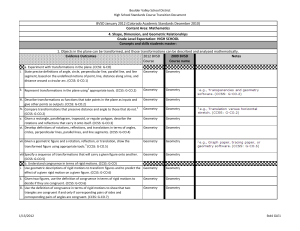
HS Standards Course Transition Document 2012
... Course Course name name a. Experiment with transformations in the plane. (CCSS: G-CO) i. State precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. (CCSS: G ...
... Course Course name name a. Experiment with transformations in the plane. (CCSS: G-CO) i. State precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. (CCSS: G ...
Circle Geometry
... Illogical and sloppy proofs result in your losing marks in assessments and examinations. ...
... Illogical and sloppy proofs result in your losing marks in assessments and examinations. ...
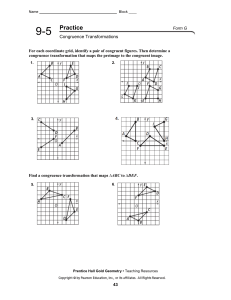
Geometry 15.09.16 CP1
... 1-4 Pairs of Angles In a circle a diameter is a segment that passes through the center of the circle and whose endpoints are on a circle. A radius of a circle is a segment whose endpoints are the center of the circle and a point on the circle. The circumference of a circle is the distance around th ...
... 1-4 Pairs of Angles In a circle a diameter is a segment that passes through the center of the circle and whose endpoints are on a circle. A radius of a circle is a segment whose endpoints are the center of the circle and a point on the circle. The circumference of a circle is the distance around th ...
Algorithms and Proofs in Geometry
... Any problem in geometry can easily be reduced to such terms that a knowledge of the lengths of certain straight lines is sufficient for its construction…to find required lines it is merely necessary to add or subtract other lines; or else, taking one line which I shall call unity, and having given t ...
... Any problem in geometry can easily be reduced to such terms that a knowledge of the lengths of certain straight lines is sufficient for its construction…to find required lines it is merely necessary to add or subtract other lines; or else, taking one line which I shall call unity, and having given t ...
Unit 7 Circles - Clover Park School District
... Students continue to expand their understanding of geometry by exploring geometric relationships pertaining to circles. As was the case in algebra 1 and earlier in geometry, attributes of circles observed at earlier grades will now be looked at more precisely through proof. Many of the geometric rel ...
... Students continue to expand their understanding of geometry by exploring geometric relationships pertaining to circles. As was the case in algebra 1 and earlier in geometry, attributes of circles observed at earlier grades will now be looked at more precisely through proof. Many of the geometric rel ...
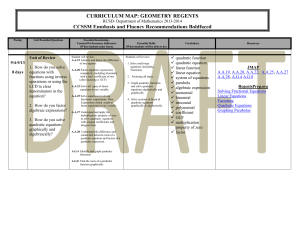
Standards addressed in Geometry Unit
... quadrants of the coordinate plane. Include use of coordinates and absolute value to find distances between points with the same first coordinate or the same second coordinate. 2. 6.G.3 – Draw polygons in the coordinate plane given coordinates for the vertices; use coordinates to find the length of a ...
... quadrants of the coordinate plane. Include use of coordinates and absolute value to find distances between points with the same first coordinate or the same second coordinate. 2. 6.G.3 – Draw polygons in the coordinate plane given coordinates for the vertices; use coordinates to find the length of a ...
H2 Angles, Circles and Tangents Introduction
... to where Christ was born (in the Levant, Eastern Mediterranean). Before the magnetic compass was discovered, early map makers would draw a small 16-pointed circle on the map indicating the 4 cardinal points and the intervening points. The 32 points of the compass rose come from the directions of the ...
... to where Christ was born (in the Levant, Eastern Mediterranean). Before the magnetic compass was discovered, early map makers would draw a small 16-pointed circle on the map indicating the 4 cardinal points and the intervening points. The 32 points of the compass rose come from the directions of the ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.