Physics 517/617 Experiment 2 R-L-C Circuits
... Measure the frequency response (i.e. voltage gain and output voltage phase shift relative to the input voltage) of the filter you built in part 1) to a sine wave. Make measurements over the frequency range 10 Hz-100 kHz (or as high as you can go). Plot the measurements with the theoretical expectati ...
... Measure the frequency response (i.e. voltage gain and output voltage phase shift relative to the input voltage) of the filter you built in part 1) to a sine wave. Make measurements over the frequency range 10 Hz-100 kHz (or as high as you can go). Plot the measurements with the theoretical expectati ...
Lab 3: Matching Networks and Tuning Stubs
... 2. Asymmetric Stubs Another PC Board in the toolbox was made to zero the conductance of a 5.6nH inductor at 1.25GHz. Measure and model the circuit. Does this circuit behave as expected? Modify the circuit with copper tape to tune to the correct frequency if necessary. Document your tuned asymmetric ...
... 2. Asymmetric Stubs Another PC Board in the toolbox was made to zero the conductance of a 5.6nH inductor at 1.25GHz. Measure and model the circuit. Does this circuit behave as expected? Modify the circuit with copper tape to tune to the correct frequency if necessary. Document your tuned asymmetric ...
Introduction to Electromagnetism
... Ex: (G.30.8.p.766) At t=0, an inductor (L = 40 mH = milliHenry) is placed in series with a resistance R = 3 W (ohms) and charged capacitor C = 5 mF (microFarad). (a) Show that this series will oscillate. (b) Determine its frequency with and without the resistor. © What is the time for the charge amp ...
... Ex: (G.30.8.p.766) At t=0, an inductor (L = 40 mH = milliHenry) is placed in series with a resistance R = 3 W (ohms) and charged capacitor C = 5 mF (microFarad). (a) Show that this series will oscillate. (b) Determine its frequency with and without the resistor. © What is the time for the charge amp ...
The two problems below replace Diefenderfer & Holton, Chapter 3, Problem 24: D&H problem 324 as stated has a typo. There should be an absolute value bracket around the right
... side, and a "j" in front of the CR2 term. Here is the actual problem that you should solve, the first part is the typocorrected DH, and the second part is additional: 1. Derive the following transfer function expression for the circuit of Figure E: vo vs ...
... side, and a "j" in front of the CR2 term. Here is the actual problem that you should solve, the first part is the typocorrected DH, and the second part is additional: 1. Derive the following transfer function expression for the circuit of Figure E: vo vs ...
resonance experiment
... across the inductor are equal, so the circuit looks like a resistor. No energy is dissipated at resonance. We looked at a typical resonant LCR circuit as shown in the diagram below. The values of the capacitor, inductor and resistor were 4700Picofarads, 1MH and either 33ohms or 330ohms depending on ...
... across the inductor are equal, so the circuit looks like a resistor. No energy is dissipated at resonance. We looked at a typical resonant LCR circuit as shown in the diagram below. The values of the capacitor, inductor and resistor were 4700Picofarads, 1MH and either 33ohms or 330ohms depending on ...
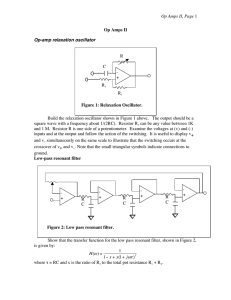
Op Amps II, Page R C -
... Figure 1: Relaxation Oscillator. Build the relaxation oscillator shown in Figure 1 above. The output should be a square wave with a frequency about 1/(2RC). Resistor R1 can be any value between 1K and 1 M. Resistor R is one side of a potentiometer. Examine the voltages at (+) and (-) inputs and at t ...
... Figure 1: Relaxation Oscillator. Build the relaxation oscillator shown in Figure 1 above. The output should be a square wave with a frequency about 1/(2RC). Resistor R1 can be any value between 1K and 1 M. Resistor R is one side of a potentiometer. Examine the voltages at (+) and (-) inputs and at t ...
Assignment-2 File - Shankersinh Vaghela Bapu Institute of Technology
... SINGLE PHASE AC CIRCUIT 1) Explain with the aid of a phasor diagram the phenomenon of resonance in a circuit containing an inductor, a capacitor and a resistor in series. 2) Distinguish between (i) apparent power (ii) active power and (iii) reactive power 3) Prove that average power consumption in p ...
... SINGLE PHASE AC CIRCUIT 1) Explain with the aid of a phasor diagram the phenomenon of resonance in a circuit containing an inductor, a capacitor and a resistor in series. 2) Distinguish between (i) apparent power (ii) active power and (iii) reactive power 3) Prove that average power consumption in p ...
4. RLC series resonance
... 1. Make the connections as per the circuit diagram. 2. Switch on the supply keeping source frequency of the signal generator at lowest. 3. Take the value of frequency & current as per the observation table. ...
... 1. Make the connections as per the circuit diagram. 2. Switch on the supply keeping source frequency of the signal generator at lowest. 3. Take the value of frequency & current as per the observation table. ...
AC_2014mar10
... • Real inductors often have significant resistance (RL) because they contain many meters of wire in their coils. • The signal generator as well has some resistance inside it (Rs is approximately 50 ohms). In our circuit, Rd represents variable decade resistor. • In the formulas, the resistance “R” r ...
... • Real inductors often have significant resistance (RL) because they contain many meters of wire in their coils. • The signal generator as well has some resistance inside it (Rs is approximately 50 ohms). In our circuit, Rd represents variable decade resistor. • In the formulas, the resistance “R” r ...
The RLC Circuit
... – Q corresponds to x; L corresponds to m; R corresponds to the damping constant b; and 1/C corresponds to 1/k, where k is the force constant of the spring. • The quantitative solution for the quadratic equation involves more knowledge of differential equations than we possess, so we will stick with ...
... – Q corresponds to x; L corresponds to m; R corresponds to the damping constant b; and 1/C corresponds to 1/k, where k is the force constant of the spring. • The quantitative solution for the quadratic equation involves more knowledge of differential equations than we possess, so we will stick with ...
RLC circuit

A RLC circuit is an electrical circuit consisting of a resistor (R), an inductor (L), and a capacitor (C), connected in series or in parallel. The name of the circuit is derived from the letters that are used to denote the constituent components of this circuit, where the sequence of the components may vary from RLC.The circuit forms a harmonic oscillator for current, and resonates in a similar way as an LC circuit. Introducing the resistor increases the decay of these oscillations, which is also known as damping. The resistor also reduces the peak resonant frequency. Some resistance is unavoidable in real circuits even if a resistor is not specifically included as a component. An ideal, pure LC circuit is an abstraction used in theoretical considerations.RLC circuits have many applications as oscillator circuits. Radio receivers and television sets use them for tuning to select a narrow frequency range from ambient radio waves. In this role the circuit is often referred to as a tuned circuit. An RLC circuit can be used as a band-pass filter, band-stop filter, low-pass filter or high-pass filter. The tuning application, for instance, is an example of band-pass filtering. The RLC filter is described as a second-order circuit, meaning that any voltage or current in the circuit can be described by a second-order differential equation in circuit analysis.The three circuit elements, R,L and C can be combined in a number of different topologies. All three elements in series or all three elements in parallel are the simplest in concept and the most straightforward to analyse. There are, however, other arrangements, some with practical importance in real circuits. One issue often encountered is the need to take into account inductor resistance. Inductors are typically constructed from coils of wire, the resistance of which is not usually desirable, but it often has a significant effect on the circuit.