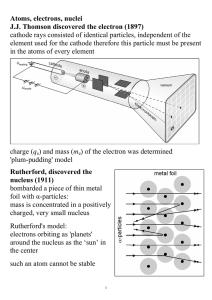
InorgCh2.1
... a) Rutherford and Moseley quickly discovered the charge of the nucleus i. Electron beams aimed at an element caused X-rays to be emitted ii. The square root of the X-ray frequency emitted had a linear relationship with about half of the atomic mass of the element iii. This number was clearly Z, the ...
... a) Rutherford and Moseley quickly discovered the charge of the nucleus i. Electron beams aimed at an element caused X-rays to be emitted ii. The square root of the X-ray frequency emitted had a linear relationship with about half of the atomic mass of the element iii. This number was clearly Z, the ...
Problem set 2
... from the origin and with finite energy E < 0) for such a particle. h2i 3. Write the Hamiltonian and Hamilton’s equations in spherical coordinates for a particle with zero angular momentum in the above potential. h2i 4. What are the cyclic coordinates and conserved momenta? h1i 5. Reduce hamilton’s e ...
... from the origin and with finite energy E < 0) for such a particle. h2i 3. Write the Hamiltonian and Hamilton’s equations in spherical coordinates for a particle with zero angular momentum in the above potential. h2i 4. What are the cyclic coordinates and conserved momenta? h1i 5. Reduce hamilton’s e ...
Chapter 8 Study Guide
... a. Chemists discovered that if two or more different compounds are composed of the same elements, the ratio of the masses of the second element is always a ratio of small whole numbers. This example illustrates the law of multiple proportions ...
... a. Chemists discovered that if two or more different compounds are composed of the same elements, the ratio of the masses of the second element is always a ratio of small whole numbers. This example illustrates the law of multiple proportions ...
l - Evergreen
... • Thomson discovered electron, invented plum-pudding model • Rutherford observed nuclear scattering, invented orbital atom • Bohr quantized angular momentum, improved H atom model. • Bohr model explained observed H spectra, derived En = E/n2 and phenomenological Rydberg constant • Quantum numbers n, ...
... • Thomson discovered electron, invented plum-pudding model • Rutherford observed nuclear scattering, invented orbital atom • Bohr quantized angular momentum, improved H atom model. • Bohr model explained observed H spectra, derived En = E/n2 and phenomenological Rydberg constant • Quantum numbers n, ...
Take silver atoms with an electron that has a moment of µz = −g e(e
... should have different total spins and then they should respond differently to magnetic fields. In the Stern-Gerlach experiment they send these atoms in the x direction between magnets one above the other, where z is the up/down direction and the magnets have length l (not to be mixed up with the qua ...
... should have different total spins and then they should respond differently to magnetic fields. In the Stern-Gerlach experiment they send these atoms in the x direction between magnets one above the other, where z is the up/down direction and the magnets have length l (not to be mixed up with the qua ...
SCHRÖDINGER EQUATION FOR A PARTICLE ON A CURVED SPACE AND SUPERINTEGRABILITY
... Abstract. A formulation of quantum mechanics on spaces of constant curvature is studied by quantizing the Noether momenta and using these to form the quantum Hamiltonian. This approach gives the opportunity of studying a superintegrable quantum system. It is shown there are three different ways of o ...
... Abstract. A formulation of quantum mechanics on spaces of constant curvature is studied by quantizing the Noether momenta and using these to form the quantum Hamiltonian. This approach gives the opportunity of studying a superintegrable quantum system. It is shown there are three different ways of o ...
Quantum Mechanical Model
... The Quantum Model of the Atom Directions: Complete the following notes and charts as you read through section 4.2 in your textbook. ...
... The Quantum Model of the Atom Directions: Complete the following notes and charts as you read through section 4.2 in your textbook. ...
100610 chem a GALL
... number of one because it has one proton. Hydrogen only SOMETIMES has a neutron... The average mass of a hydrogen atom is 1.0079 amu. ...
... number of one because it has one proton. Hydrogen only SOMETIMES has a neutron... The average mass of a hydrogen atom is 1.0079 amu. ...
general properties of the solution: quantum numbers:
... probability density at the nucleus (r = 0) - l > 0 (p, d, f, g, ...) wave functions have a node in the probability density at (r = 0) - as a result the average is non-zero giving the
electron angular momentum
- electron probability density:
- probability to find electron in Volume element dV
...
... probability density at the nucleus (r = 0) - l > 0 (p, d, f, g, ...) wave functions have a node in the probability density at (r = 0) - as a result the average
QUASICLASSICAL AND QUANTUM SYSTEMS OF ANGULAR FOR QUANTUM-MECHANICAL MODELS WITH SYMMETRIES
... nucleons, systems of quantized angular momenta of rotating extended objects like molecules. Secondly, the other promising area of applications is Schrödinger quantum mechanics of rigid body with its often rather unexpected and very interesting features. Even within this Schrödinger framework the alg ...
... nucleons, systems of quantized angular momenta of rotating extended objects like molecules. Secondly, the other promising area of applications is Schrödinger quantum mechanics of rigid body with its often rather unexpected and very interesting features. Even within this Schrödinger framework the alg ...
Lesson 2 - The Bohr and Quantum Mechanical Model of the Atom
... Lesson 2 The Bohr and Quantum Mechanical Model of the Atom ...
... Lesson 2 The Bohr and Quantum Mechanical Model of the Atom ...
Chapter 12 Worksheet
... 8. Calculate the wavelengths (nm) emitted for the following electronic transitions in a Li2+ ion. a. n = 5 n = 3 b. n = 3 n = 1 9. An excited hydrogen atom with an electron in n = 5 state emits light having a frequency of 6.9 x 1014 s-1. Determine the principal quantum level (n) for the final st ...
... 8. Calculate the wavelengths (nm) emitted for the following electronic transitions in a Li2+ ion. a. n = 5 n = 3 b. n = 3 n = 1 9. An excited hydrogen atom with an electron in n = 5 state emits light having a frequency of 6.9 x 1014 s-1. Determine the principal quantum level (n) for the final st ...
stationary state
... • When an electron is in one of the quantized orbits, it does not emit any electromagnetic radiation; thus, the electron is said to be in a stationary state. • The electron can make a discontinuous emission, or quantum jump, from one stationary state to another. During this transition it does emit r ...
... • When an electron is in one of the quantized orbits, it does not emit any electromagnetic radiation; thus, the electron is said to be in a stationary state. • The electron can make a discontinuous emission, or quantum jump, from one stationary state to another. During this transition it does emit r ...
Section 13.2 - CPO Science
... line in a spectroscope. • A spectroscope is a device that spreads light into its different colors. ...
... line in a spectroscope. • A spectroscope is a device that spreads light into its different colors. ...
9/25 - SMU Physics
... In particle physics, we estimate some particle’s lifetime by measuring its energy (mass) uncertainty. example: the particle π0 has a mass of 134.98 MeV, decays into two photons. Its mean lifetime τ = 8.4×10-17 sec, derived from its width of 0.0006 MeV in its mass measurement. Et ...
... In particle physics, we estimate some particle’s lifetime by measuring its energy (mass) uncertainty. example: the particle π0 has a mass of 134.98 MeV, decays into two photons. Its mean lifetime τ = 8.4×10-17 sec, derived from its width of 0.0006 MeV in its mass measurement. Et ...
Hydrogen atom
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively charged proton and a single negatively charged electron bound to the nucleus by the Coulomb force. Atomic hydrogen constitutes about 75% of the elemental (baryonic) mass of the universe.In everyday life on Earth, isolated hydrogen atoms (usually called ""atomic hydrogen"" or, more precisely, ""monatomic hydrogen"") are extremely rare. Instead, hydrogen tends to combine with other atoms in compounds, or with itself to form ordinary (diatomic) hydrogen gas, H2. ""Atomic hydrogen"" and ""hydrogen atom"" in ordinary English use have overlapping, yet distinct, meanings. For example, a water molecule contains two hydrogen atoms, but does not contain atomic hydrogen (which would refer to isolated hydrogen atoms).