Download Ch04 - Skylight Publishing

Java Methods
A & AB
Object-Oriented Programming
and Data Structures
Maria Litvin ● Gary Litvin
chapter  4
Algorithms
Copyright © 2006 by Maria Litvin, Gary Litvin, and Skylight Publishing. All rights reserved.
Objectives:
•
•
•
•
•
Understand general properties of algorithms
Get familiar with pseudocode and flowcharts
Learn about iterations and recursion
Learn about working with lists
Learn basic facts about OOP
4-2
Define Algorithm...
• Hard to define formally
• A more or less compact, general, and
abstract step-by-step recipe that describes
how to perform a certain task or solve a
certain problem.
• Examples:



Long division
Euclid’s Algorithm for finding the greatest common
factor (circa 300 BC)
Binary Search (guess-the-number game)
4-3
Tools for Describing
Algorithms
• Pseudocode


A sequence of statements, more precise
notation
Not a programming language, no formal
syntax
• Flowcharts

Graphical representation of control flow
4-4
Example: calculate 12 + 22 + ... + n2
• Pseudocode
Input: n
sum  0
i1
Repeat the following
three steps while i  n:
sq  i * i
sum  sum + sq
ii+1
AB
Set A to the
value of B
Output: sum
4-5
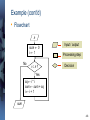
Example (cont’d)
• Flowchart
n
sum  0
i1
No
in?
Input / output
Processing step
Decision
Yes
sq  i * i
sum  sum + sq
ii+1
sum
4-6
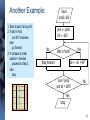
Another Example:
1. Start at pos0, facing dir0
2. If wall in front,
turn 90º clockwise
else
go forward
3. If not back to initial
position / direction
proceed to Step 2
else
stop
Input:
pos0, dir0
pos  pos0
dir  dir0
No
Yes
Wall in front?
dir  dir + 90º
Step forward
pos = pos0
and dir = dir0?
No
Yes
Stop
4-7
Variables
• Algorithms usually work with variables
• A variable is a “named container”
• A variable is like a slate on which a value can
be written and later erased and replaced with
another value
sum
sum  sum + sq
4-8
Properties of Algorithms
• Compactness: an algorithm can use iterations
or recursion to repeat the same steps multiple
times
• Generality: the same algorithm applies to any
“size” of task or any input values
• Abstractness: an algorithm does not depend
on a particular computer language or platform
(although it may depend on the general
computing model)
4-9
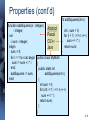
Properties (cont’d)
Input: n
sum  0
i1
Repeat the following
three steps while i  n:
sq  i * i
sum  sum + sq
ii+1
Output: sum
General: works for any n
Compact: the same length
regardless of n, thanks to
iterations  the algorithm
repeats the same
instructions many times, but
with different values of the
variables
(The “running time” depends on n, of course)
4-10
Properties (cont’d)
int addSquares(int n)
{
int i, sum = 0;
for (i = 1; i <= n; i++)
sum += i * i;
return sum;
}
function addSquares(n : integer)
Abstract:
: integer;
Pascal
var
i, sum : integer;
C/C++
begin
Java
sum := 0;
for i := 1 to n do begin public class MyMath
sum := sum + i * i
{
end;
public static int
addSquares := sum;
addSquares(int n)
end;
{
int sum = 0;
for (int i = 1; i <= n; i++)
sum += i * i;
return sum;
}
}
4-11
Iterations
• Repeat the same sequence of
instructions multiple times
• Start with initial values of variables
• Values of some of the variables change
in each cycle
• Stop when the tested condition
becomes false
• Supported by high-level programming
languages
4-12
Iterations: while Loop in Java
while (<this condition holds>)
{
... // do something
}
For example:
while (i <= n)
{
sum += i * i; // add i * i to sum
i++;
// increment i by 1
}
4-13
Iterations: for Loop in Java
for (<initial setup>; <as long as this condition holds>;
<adjust variable(s) at the end of each iteration>)
{
... // do something
}
For example:
Increment i
by 1
for ( int i = 1; i <= n; i++)
{
sum += i * i; // add i * i to sum
}
4-14
Recursion
• A recursive solution describes a procedure
for a particular task in terms of applying the
same procedure to a similar but smaller task.
• Must have a base case when the task is so
simple that no recursion is needed.
• Recursive calls must eventually converge to
a base case.
4-15
Recursion: an Example
Procedure: Climb steps
Base case: if no steps
to climb  stop
Recursive case: more
steps to climb 
1. Step up one step
2. Climb steps
4-16
Recursive Methods
• A recursive method calls itself
• Must have a base case (can be implicit)
• Example:
public class MyMath
{
public static int addSquares (int n)
{
if (n == 0)
// if n is equal to 0
return 0;
else
return addSquares (n - 1) + n * n;
}
}
Base case
Calls itself
(with a smaller
value of the
parameter)
4-17
Recursion: How Does it Work
• Implemented on a computer as a form of
iterations, but hidden from the programmer
• Assisted by the system stack
Base case
addSquares (0)
0
0
addSquares (1)
1
1
addSquares (2)
2
5
addSquares (3)
14
3
4
addSquares (4)
30
4-18
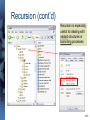
Recursion (cont’d)
Recursion is especially
useful for dealing with
nested structures or
branching processes
4-19
Recursion (cont’d)
totalBytes (folder)
{
count  0
(This is pseudocode,
not Java!)
for each item X in folder
{
Base case
if X is a file
count  count + the number of bytes in X
else (if X is a folder)
count  count + totalBytes(X)
}
return count
}
4-20
Euclid’s Algorithm
• Finds the greatest common factor (GCF) of
two positive integers
• Circa 300 BC
4-21
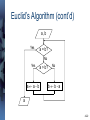
Euclid’s Algorithm (cont’d)
a, b
Yes
a = b?
No
Yes
aa-b
a > b?
No
bb-a
a
4-22
Euclid’s Algorithm (cont’d)
• With iterations
public static int gcf (int a, int b)
{
while (a != b) // a not equal to b
{
if (a > b)
a -= b; // subtract b from a
else
b -= a; // subtract a from b
}
return a;
}
• With recursion
public static int gcf (int a, int b)
{
if (a == b) // if a equals b
return a;
Base case
if (a > b)
return gcf( a - b, b);
else // if a < b
return gcf(a, b - a);
}
4-23
Working with Lists
• A list is a data structure in which the items are
numbered
Dan
0
Fay
1
Cal
2
Ben
3
Guy
4
Amy
5
Eve
6
In Java, the elements
are counted from 0
• We know how to get to the i-th item
• We know how to get from one item to the next
quickly
4-24
List Traversal


Start at the first element
While more elements remain
process the next element
for (int i = 0; i < list.length; i++)
System.out.println (list [ i ]);
for (String word : list)
System.out.println (word);
Increment i
by 1
Java’s “for each” loop
(a.k.a. enhanced for
loop)
4-25
Sequential Search
Dan
0
Fay
1
Cal
2
Ben
3
Guy
4
Amy
5
Amy?
Amy?
Amy?
Amy?
Amy?
Amy!
Eve
6
• The number of comparisons is proportional to
n, where n is the length of the list
4-26
Binary Search
• “Divide and conquer” algorithm
• The elements of the list must be arranged
in ascending (or descending) order
• The target value is always compared with
the middle element of the remaining
search range
4-27
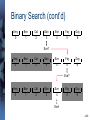
Binary Search (cont’d)
Amy
0
Ben
1
Cal
2
Dan
3
Eve
4
Fay
5
Guy
6
Eve
4
Fay
5
Guy
6
Eve?
Amy
0
Ben
1
Cal
2
Dan
3
Eve?
Amy
0
Ben
1
Cal
2
Dan
3
Eve
4
Fay
5
Guy
6
Eve!
4-28
Search:
Sequential
Binary
• The list can be in
random order
• The number of
comparisons is
proportional to n
• The list must be sorted
(e.g., in ascending order)
• The number of
comparisons is
proportional to log2 n
• For a list of 1,000,000
• For a list of 1,000,000
elements takes, on
average, 500,000
comparisons
elements takes, on
average, only 20
comparisons
4-29
Review:
•
•
•
•
•
Why algorithms often use iterations?
How is pseudocode different from Java code?
Name three basic shapes used in flowcharts.
Explain how variables are used in iterations.
Which Java statements can be used to express
iterations?
4-30
Review (cont’d):
• What is called a base case in recursion?
• Suppose we define “word” as a sequence of letters.
Turn this into a recursive definition.
• When does Binary Search apply?
• How many comparisons, on average, are needed to
find one of the values in a list of 1000 elements using
Sequential Search? Binary Search?
4-31