Download Young`s Double Slits

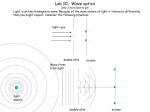
Physics 1 – Young’s Double Slits
Young’s Double Slits
Aims
 To investigate the wave-like nature of light.
 To perform quantitative measurements of interference.
Part 1: Tutorial question (15mins)
 Two narrow parallel vertical slits in a screen, at a small distance d apart centre-tocentre, are used to provide equal sources of light of wavelength  and a second
screen is placed at a large distance R in front of the slits. Prove that:
1.1
the optical path difference at the mth bright interference fringe is given
by
r2  r1  d sin   m,
[1.1]
where m is an integer;
1.2
the separation between the mth bright fringe and the centre fringe on the
screen is given by:
y
m R
.
d
[1.2]
State any assumptions made.
1.3
We observe the distance between any two bright fringes to be 1.0 mm.
What is the separation between the slits if the wavelength of light is
 = 532 nm and the distance to the screen is R = 1.0 m?
r1
S1

d
y
I
r2
S2
R

Figure 1




1
Physics 1 – Young’s Double Slits

Part 2: Observing interference with a laser (20mins)
Laser Safety
WARNING: IT IS IMPERATIVE THAT YOU READ AND UNDERSTAND THE
FOLLOWING INFORMATION BEFORE ATTEMPTING THE EXPERIMENT
DETAILED BELOW. IF YOU HAVE ANY QUESTIONS PLEASE CONSULT A
LABORATORY DEMONSTRATOR.
Operational Hazard – Semiconductor laser diodes
The two laser sources you will be using emit green and red visible light. Both are
categorised as class 2 sources and thus defined to be eye safe (i.e. the human blink
reflex will be sufficient to prevent damaging exposure), having a power output <
1mW. However, you must never look directly into the beam path or stare at the laser
output port, and you must never point the laser beam at yourself or anyone else.
In this part of the experiment you will determine the spacing of the two slits on the
slide from the interference pattern of green light at a known wavelength.
 Firstly, affix the green laser pen to the clamp stand, it may be useful to use a cable
tie to keep the button depressed.
 Place this at one end of the horizontal track and align the beam so that it is centred
on the zero position on the ruled screen at the other end.
 Now, place the slide saddle on the track in front of the beam, so that a diffraction
pattern appears on the screen.
 Note the positions of the two saddles, and deduce their separation.
 Measure the separation between adjacent maxima on the ruler screen.
2.1
Knowing that the wavelength of the light is 532nm, and using your results
from part 1, calculate the slit separation d.
2.2
Deduce the error on your result using the following equation
d y
,

d
y
[2.1]
where y is the error on your measurement of y.
Part 3: Calculating the wavelength of red laser light (15 mins)
You will now use your results from part 2 to determine the wavelength of the red laser
light and compare it with the values shown on the laser pointer.
 Replace the green laser pen with the red one and again affix it to the clamp stand.
 Remove the slide saddle and align the light beam so that it is centred on the zero
position.
 Place the slide saddle back on the track in the same position as before.
 You should observe a similar diffraction pattern.
2
Physics 1 – Young’s Double Slits
3.1
What is different about the image formed on the screen? Explain why this is
the case.
 Rearrange equation 1.2 to show the dependence of wavelength on maxima
separation y.
 Measure the separation of adjacent maxima.
3.2
Now calculate the wavelength of the red light. Does this compare well with
that stated on the laser of 630-680nm?
3.3
Deduce the error on your result using the following equation:
2
  
 d   y 

 
    ,
  
 d   y 
2
2
where dand y are the errors on wavelength, slit seperation and maxima
seperation respectively.
Part 4: Using a diffraction grating (Optional)
 Replace the double slit grating with a diffarction grating.
4.1
What pattern do you observe? Sketch the pattern.
Further work 
The following questions are related to the topic covered by this experimental tutorial.
L60, L61 and L62 from the examples book
3
Physics 1 – Young’s Double Slits
Demonstrators' Answers, Hints, Marking Scheme and Equipment List
Marking Scheme
Section
1.1
1.2
1.3
2.1
2.2
3.1
3.2
3.3
Discretionary mark
TOTAL
Mark
1
1
1
1
1
1
1
1
2
10
Answers
1.1
For bright fringes there must be constructive interference, so the path
difference between r1 and r2 must be an integer number of wavelengths and
from Pythagoras the path difference is also equal to d sin.
1.2
1.3
assuming for small angles: sintany/R
y
 d  m
R
mR
y 
d
0.53 mm
Part 2 Constructive interference: r2  r1  d sin   m; m  0,1,2,...
3.1

nR 7  532  10 9  1.3
d sin   n  d 

 0.242 mm
y
20  10 3
y
1
Error: d 
d 
 0.242  0.01 mm  d  0.24  0.01 mm
y
20
The wavelength of red light is larger so the seperation between maxima will
be reduced.
dy
Rn
3.2
d y 0.242  10 3  14.5  10 3

 675 nm
Constructive interference:  
Rn
1.3  4
3.3
Error:
4
Physics 1 – Young’s Double Slits
 d   y 
   
   
 d   y 
2
2
2
2
 1   1 
 675    

 24   14.5 
 675  0.0806  54 nm    675  54 nm
since one can read the scale to an accuracy of 1mm.
4.1
Equipment List:
Optical track
2 x optical track saddles
Ruler screen
Double slit slide
Green laser pen
Red laser pen
Clamp stand with boss head
Peg or 2 x cable ties
5