* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Relativity Problem Set 7 - Solutions Prof. J. Gerton October 24, 2011
Casimir effect wikipedia , lookup
Renormalization group wikipedia , lookup
Renormalization wikipedia , lookup
X-ray fluorescence wikipedia , lookup
Electron configuration wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Mössbauer spectroscopy wikipedia , lookup
Atomic orbital wikipedia , lookup
Canonical quantization wikipedia , lookup
X-ray photoelectron spectroscopy wikipedia , lookup
Wave–particle duality wikipedia , lookup
Matter wave wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Particle in a box wikipedia , lookup
Electron scattering wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
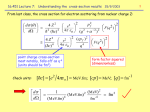
Relativity Problem Set 7 - Solutions Prof. J. Gerton October 24, 2011 Problem 1 (10 pts.) Quantization of the Bohr model In Bohr’s model , the velocity of the electron is quantized as vn = α c/n, where α = 1/137 is the fine structure constant. Since αc = 2.19 × 106 m/s, we see that only the velocities in (b) and (d) are allowed, being given by the above relation with n = 1 and n = 2 respectively. The quantities in (a) and (c) are not associated with an integer quantum number, so they are not allowed. Problem 2 (10 pts.) Lyman spectrum An electron de-exciting in a Hydrogen atom from a state of quantum number ni to a final state with nf = 1 emits a photon of frequency hν = Eni − E1 . (1) Since the energy spectrum of the Hydrogen is α2 me c2 13.6eV =− , 2 2n n2 (2) 1 α 2 m e c2 1 −1 = 1− 2 . n2i 2 ni (3) En = − we have α2 me c2 hν = − 2 Since ν = c/λ, we finally have 1 α 2 m e c2 = λ 2hc 1 1− 2 ni . (4) The Rydberg constant is thus R= α 2 m e c2 . 2hc 1 (5) 2 Problem 3 (10 pts.) Positronium The electron and the positron are a distance r apart, and they orbit around their mutual center of mass which is at a distance r/2. Each particle has mass me and velocity v. We use the Bohr-Sommerfeld quantization rule for the angular momentum L = n~, (6) where n is an integer, also known as the principal quantum number. Each particle has angular momentum me vr/2, so the total angular momentum is L = me vr and rme v = n~. (7) Another equation is found by equating the centripetal force Fc and the electromagnetic force Fe . We have 2me v 2 v2 = , (8) Fc = me r/2 r and e2 α ~c Fe = = 2 , (9) 2 4π0 r r where α ≈ 1/137 is called the fine structure constant. Equating Fc = Fe , we find the radius α ~c (10) r= 2me v 2 Solving Eqs. (7) and (10) for r, we find r= 2n2 ~c . αme c2 (11) We now find the energy spectrum E. The total energy E is given by the sum of the kinetic energy and of the potential energy. In a Coulomb potential, E = U/2 (the so-called virial theorem, valid also in classical mechanics). So, U α~c α2 me c2 E(= En ) = =− =− . (12) 2 2r 4n2 In the last equation we have used the expression for the radius in Eq. (11). The label n in En is added so that it is clear that the energy is quantized in this system, thanks to the quantization of the angular momentum. Plugging in numbers, 6.81 eV . (13) n2 The energy spectrum is proportional to n2 as in the Hydrogen atom case, which is obvious because we are still treating a Coulomb field, but the number of the fundamental level E0 = 6.81 eV is different from the fundamental level of the Hydrogen system. Positronium has long being theoretically predicted and described, but only recently it has been possible to actually create this system. En = − course name PS # 3 Problem 4 (10 pts.) Rutherford scattering (a) The α particle stops when its initial kinetic energy is equal to the electrostatic potential energy, so Qα QAu K=U = . (14) 4π0 D The potential energy is Qα QAu (+2e) (+79e) = . 4π0 D 4π0 D U= (15) Using the numerical value e2 = 1.438 MeV fm, 4π0 we have U = 1.438 MeV fm fm (2) (79) = 227.2 MeV . D D (16) (17) Equating U with K, we obtain D = 8.4 fm. (18) This is an upper limit on the size of the Gold nucleus. In practice, this is larger than the actual size of such nucleus, that can be estimated as 1.3 fm (A)1/3 ≈ 7.5 fm, where A = 197 for Gold. (b) We use the equation derived in the lecture, in the form b= Qα QAu 1 . 8π0 K tan θ/2 (19) (+2e) (+79e) 1 = 7.3 fm. 2 (27 MeV) tan 30o (20) Plugging in numbers, we have b = 1.438 MeV fm Problem 5 (10 pts.) Geiger-Marsden experiment (a) We use the same reasoning as in Problem 1, part (a). Equating U with K = 7.7 MeV, we find fm 7.7 MeV = 227.2 MeV , (21) D from which the upper value for the radius is D = 29.5 fm. course name PS # 4 (b) We assume that each Gold nucleus is packed in a sphere of radius r < D, thus of volume 4π 3 D = 1.075 × 105 fm3 . (22) V < 3 (Using a cube to pack up the atom works as fine, for the estimate). Using u = 1.661 × 10−27 Kg, each Gold nucleus has a mass mAu = 3.271 × 10−25 kg (we neglect the masses of the electrons). So, the density has a lower value ρ= 3.271 × 10−25 kg mAu 15 3 > 3 = 3.043 × 10 kg/m . 5 V 1.075 × 10 fm (23) This is the typical order of magnitude for nuclear matter density. course name PS #