Download PHY481: Electrostatics Introductory E&M review (2) Lecture 2

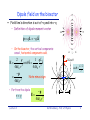
PHY481: Electrostatics
Introductory E&M review (2)
Lecture 2
Carl Bromberg - Prof. of Physics
Electric field from point charges
 The electric field Ep generated by point charges at
point P is the vector sum of Ei from each charge:
1 n qi
Ep =
r̂
∑
2 i
4πε 0 i=1 ri
 Find electric field at the origin due to the three charges q1-3
on corners of a square with side a.
1
Ep =
4πε 0
⎡ q1
q2 ⎛ ĵ + k̂ ⎞ q3
⎢ − 2 k̂ − 2 ⎜⎝
⎟⎠ − 2
2a
a
⎣ a
2
(
−1 ⎡
=
q +
2 ⎣ 1
4πε 0 a
Lecture 2
2
4
) (
q2 k̂ + q3 +
2
4
⎤
ĵ⎥
⎦
)
q2 ĵ⎤⎦
Carl Bromberg - Prof. of Physics
1
Dipole field on the bisector
 Field line’s direction is out of +q and into –q
– Definition of dipole moment vector
p = qL = −qLî
– On the bisector, the vertical components
cancel, horizontal components add.
2 q
1 qL
E=
cosθ î =
î
2
3
4πε 0 r
4πε 0 r
−p
=
Note minus sign
3
4πε 0 r
– Far from the dipole
r≈y
Lecture 2
−p
E=
4πε 0 y 3
y
2Ecosθ
r
+
θ
cosθ =
r
p
–
L/2
r
x
L
Carl Bromberg - Prof. of Physics
2
Uniformly charged infinite plane
 For an infinite horizontal plane the only reasonable direction for
the electric field E is vertical.
 Electric field can be determined by integrating over the charge
distribution (try it yourself). It is not too surprising that the
field is the same at all distances above the plane.
z
σ
E=
k̂ (above)
2ε 0
σ
E=−
k̂ (below)
2ε 0
E
σ
x
y
 The change in the electric field going from below to above
ΔE =
Lecture 2
σ
ε0
Carl Bromberg - Prof. of Physics
3
Parallel charge sheets
 Two infinite sheets of charge are separated by a
constant distance d. One sheet has a charge density
+σ and the other a charge density –σ.
– Outside, the electric fields point in opposite directions
E
σ
−σ
– Between the sheets the electric fields point in the same
direction.
Eoutside
σ
σ
=
î +
(− î) = 0 Outside plates field is zero
2ε 0
2ε 0
Einside
σ
= î
ε0
Field between the plates
 Uniform electric field E, applies a
constant force on a small particle with
charge q and mass m.
Lecture 2
F q
F = qE and a = = E
m m
Carl Bromberg - Prof. of Physics
4
Torque on a small electric dipole
 An electric dipole p in a uniform electric field
E experiences a net torque Ν and no net force.
y
– Choose coordinates where p and E lie in the x/y
plane. p and E have an angle θ between them.
p
E
Ν = p × E = pE sin θ (−k̂)
–qE
+
qE
θ
x
−
 In addition to a torque, an electric field E with
a divergence will generate, a net force F on an
electric dipole, p :
Cartesian
coordinates
Lecture 2
F = pi
∂E j
∂xi
ê j
General expression needs
operators to be covered later
Carl Bromberg - Prof. of Physics
5
Energy of dipole in electric field
 Potential energy U of the
field E:
p
E
–qE
electric dipole p in uniform electric
y
+
qE
θ
x
−
U = −p ⋅ E = − pE cosθ
Lecture 2
Carl Bromberg - Prof. of Physics
6
Gauss’s Law
 Electric field passing through a closed (mathematical) surface
– A surface enclosing NO net charge has a zero net field leaving or
entering the surface.
– A surface enclosing a positive (negative) charge has a net field
leaving (entering) the surface proportional to the enclosed charge.
n̂
closed
surface
dA
qencl
∫S E ⋅ dA = ε 0
General expression
for Gauss’s Law
– For symmetric charge distributions, pick an enclosing surface where
E and dA are everywhere parallel to each other.
Lecture 2
Carl Bromberg - Prof. of Physics
7
Coulomb’s Law <---> Gauss’s Law
 For symmetric charge distributions, pick enclosing surfaces, so
that E and dA are are parallel to each other.
– For a point charge at the origin, use a spherical surface, radius R,
centered on the charge (makes direction of normal = radial)
Electric field at surface
q
q
E=
r̂
2
4πε 0 R
Evaluate Gauss’s
Integral

n̂ = r̂
dA = R 2 sinθ dθ dφ
q
∫S E ⋅ dA = 4πε 0 R2
π
∫R
0
2
sin θ dθ
2π
∫
0
q
dφ =
ε0
This is a “proof” that Gauss’s law follows directly from the Coulomb
Force Law for point charges, and their derived electric fields.
Lecture 2
Carl Bromberg - Prof. of Physics
8
Field of a line of charge - use Gauss’s Law
 Consider an infinitely long line of charge with linear
charge density λ , and a cylindrical gaussian surface.
– The electric field is parallel to the surface at the top
and bottom of the cylinder, E•dA is zero.
– The electric field is perpendicular to the surface and
therefore parallel to the surface normal.
2π
∫S E ⋅ dA = Er ∫
L
dφ ∫ dz
0
0
qencl λ L
E2π rL =
=
ε0
ε0
λ
E=
;
2πε 0 r
Lecture 2
qencl = λ L
λ
E=
r̂
2πε 0 r
Carl Bromberg - Prof. of Physics
9
Field of a charged spherical shell - Gauss’s Law
 Consider a radius R spherical shell with surface charge density σ.
– A spherical Gaussian surface with radius r < R, is inside the charge
surface, and encloses no charge -> Einside = 0.
– A spherical Gaussian surface with radius r > R, has the electric field
normal to its surface.
π
2π
2
E
⋅
dA
=
E
r
∫S
∫ sinθ dθ ∫ dφ
0
0
q
2
E4π r =
ε0
q = σ 4π R 2
q
q
E=
; E=
r̂
2
2
4πε 0 r
4πε 0 r
Same electric field as
charge q at the origin
Lecture 2
Carl Bromberg - Prof. of Physics
10
Uniform charge density sphere - Gauss’s Law
 Find the electric field inside of a sphere, radius R, with a
uniform charge density ρ throughout the volume.
– Pick a spherical Gaussian surface, radius r,
inside the charged sphere
π
2π
2
E
⋅
dA
=
Er
∫S
∫ sinθ dθ ∫ dφ
0
0
3
q
Qr
E4π r 2 = encl =
ε0
ε 0 R3
ρ=Q/
Qr
Qr
E=
; E=
r̂
3
3
4πε 0 R
4πε 0 R
qencl = ρ
(
(
3
4
π
R
3
4
πr3
3
)
)
r3
=Q 3
R
– Electric field outside of a sphere
Q
E=
r̂
2
4πε 0 r
Lecture 2
Same electric field as
charge Q at the origin
Carl Bromberg - Prof. of Physics
11
Infinite sheet (again) - Gauss’s Law
 Infinite sheet of charge with surface density σ.
– Pick a cylindrical Gaussian surface, radius r, passing through
the sheet.
– The dot product E•dA is non zero only on TWO the ends.
R
2π
∫S E ⋅ dA = 2E ∫ rdr ∫
0
qencl
2(Eπ R ) =
ε0
2
qencl = σ (π R 2 )
dφ
0
σ (π R 2 )
=
ε0
σ
σ
E=
; E=±
k̂
2ε 0
2ε 0
Lecture 2
+ above
– below
Carl Bromberg - Prof. of Physics
12