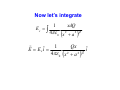* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 21
History of quantum field theory wikipedia , lookup
Magnetic monopole wikipedia , lookup
Anti-gravity wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Fundamental interaction wikipedia , lookup
Speed of gravity wikipedia , lookup
Electromagnetism wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Maxwell's equations wikipedia , lookup
Lorentz force wikipedia , lookup
Field (physics) wikipedia , lookup
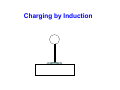
Ch. 21 Electric Charge and Electric Field • In mechanics, we used the basic property of matter called MASS. We studied how mass behaves. • In electricity, the basic concept is CHARGE. We will study how charge behaves. • Ancient Greeks discovered that when amber was rubbed with wool, it could pick up bits of straw. • The amber acquired a net electric charge. • A plastic rod that has been rubbed with fur attracts a glass rod that has been rubbed with silk. • There are two kinds of charge. The plastic rod and the silk are said to be negatively charged, and the glass rod and fur are positively charged. • Benjamin Franklin coined the sign convention. A positive charge attracts a negative charge. A negative charge repels a negative charge, and a positive charge repels a positive charge. Thus, like charges repel each other and opposite charges attract each other. Electric Charge 2 Plastic rods rubbed with a piece of fur A glass rod rubbed with silk attracts a Plastic rod rubbed with fur. Like charges repel. Opposite charges attract. The Atom • Matter is made up of atoms • Atoms consist of negatively charged electrons that orbit a nucleus. The nucleus consists of positively charged protons and neutrons (no charge). • The nucleus is on the order of 10-15 m. Electrons are on the order of 10-10 m from the nucleus. • Electrons are held within atom by attractive electric forces exerted on them by the positive nucleus. • Protons and neutrons are held together in the nucleus by a short-range, strong nuclear force that overcomes the repulsive force of the protons. Proton Neutron Electron + mp=1.673x10-27 kg 0 mn=1.675x10-27 kg - me=9.109x10-31 kg Electric Charge • Electric charge is a scalar quantity • Matter is made up of atoms that contain three particles: negatively-charged electrons, positively-charged protons, and uncharged neutrons. • These particles have mass. • The electron charge is equal and opposite in magnitude to the proton. Principle of Conservation of Charge: The algebraic sum of all the electric charges in any closed system is constant. The magnitude of charge of the electron or proton is a natural unit of charge. Charging by Induction Coulomb’s Law The magnitude of the electric force between two point charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them. qe-= 1.602 x 10-19 C F2 on 1 + q1 F=k r k= |q1q2| r2 1 =8.988 x 109 Nm2/C2 4πεo + q2 F1 on 2 If the fur and glass rod are far away from each other, do they seem to attract as strongly as when there is little distance that separates them? Electric force vs. gravitational force α α Fg Fe Fg + Fe + r 1 q2 Fe= 4πε r2 o m2 Fg=G r2 Fe/Fg = 3.1 x 1035 The Law of Electrostatic Forces seems very similar to the Law of Gravity, but gravity Always attracts. Electrical forces can either attract or repel. Electrical forces are Much stronger than gravitational forces. Principle of Superposition of Forces What happens when we have more than 2 point charges? Say we that have two charges exerting forces simultaneously on a third charge. The total force acting on that third charge is the vector sum of the forces that each charge exerts on the third charge individually. *Coulomb’s Law assumes that the charges are in a vacuum. Otherwise you have to consider the interaction of material in space with the charges. Electric Fields and Electric Forces • How does a charge q1 know that another charge q2 is present when they do not touch? (Recall that the earth exerts a force on the moon.) • We call this phenomenon action at a distance. • We answer the question by saying that q1 sets up an electric field in the space surrounding it. • At any point P in space, the field has both magnitude and direction that determine the magnitude and direction of the force on q2. Electric Field • The electric field is a vector field. It consists of a distribution of vectors. • We can visualize the electric field by imagining we are carrying around a small positive test charge around and mapping the direction of the force on it. • The electric field E at point P due to a charged object is defined as: E=F/qo • Although we used a test charge qo to define the electric field of a charged object, that field exists independently of the test charge. Let’s be careful • What if putting a test charge in the vicinity of the charges causes the charges to shift? r E = lim q →0 r F q Electric Field of a Point Charge qo r 1 |qqo| Fo= 4πε r2 o Field Point r^ q + Source Point The magnitude E of the electric field at P is: 1 |q| E = 4πε r2 o The magnitude and direction of the electric field at P is: 1 |q| ^ E = 4πε r2 r o Distribution of Charges • To calculate the field due to a charge distribution, think of the electric field for each individual point charge. • At any point P, an individual charge creates its own electric field. r A test r charge placed at P feels a force F1 = q0 E1 from charge q1. • Using the same Principle of Superposition, we can add up the total force F0 that the charge distribution exerts on q0 as the vector sum of the individual forces. r r r r r r r F0 = F1 + F2 + F3 + ... = q0 E1 + q0 E 2 + q0 E3 + ... r r F0 r r r E= = E1 + E 2 + E 3 + ... q0 Electric Field from a Ring of Charge ds We can use the Principle of Superposition but we have a continuous distribution of charge. a x P Q Consider a small portion of the ring ds. In that portion is a small amount of charge dQ that we will treat as a point charge. Calculate the total field dE that results from the charge dQ. Add up all these tiny amounts of electric field by evaluating the integral r r E = ∫ dE Consider symmetry to simplify the problem! Consider Symmetry Let’s look at a segment at the top of the ring and a segment at the bottom of the ring. These segments have the same x-component and opposite ycomponents that contribute to the electric field at point P. When we look at all the contributions to the electric field, we see that only the Electric field at point P will only be in the x-direction. ds a r = x2 + a2 α x Q P dEy dEx dE 1 dQ dE = 2 2 4πε 0 x + a 1 dQ dE x = dE cos α = 2 2 4πε 0 x + a dE x = 1 ( xdQ 4πε 0 x + a 2 2 x x +a 2 ) 3 2 2 Now let’s integrate Ex = ∫ r E = E x iˆ = 1 xdQ ( 4πε 0 x + a 1 2 ( 2 ) 3 Qx 4πε 0 x 2 + a 2 2 ) 3 2 iˆ Let’s check What happens at x=0? At x=0, E=0 What happens at x>>a? r E= Q ˆ i 2 4πε 0 x 1 The field is the same as the field for a point charge! To an observer far away, The ring looks like a point. Electric Field Lines • Electric field lines point toward negative charges and away from positive charges • We have talked about calculating the electric field at a certain point, but the electric field can vary from point to point. It is not a single vector quantity but an infinite set of vector quantities. Thus we have a vector field. • It is nice to think of the electric field in terms of electric field lines. + - Electric Field Lines • An electric field line is an imaginary line or curve drawn through a region of space so that its tangent at any point is in the direction of the electric-field vector at that point. Electric field lines give the direction of E at each point. The spacing of electric field lines tells us about the strength of the electric field at that region. If the lines are spaced closely together, the field is strong. If the lines are spaced far apart, the field is weak. • If the magnitude and direction of the electric field is the same at every point, then the electric field is uniform. (Density of electric field lines are uniformly spaced.) Field lines never intersect. Conductors • Inside a conductor: If there is an electric field inside a conductor, then every charge is acted on by the force of the electric field. The free charges then move around. Since the charges are free to move, they will be pushed to the inside surface of the conductor. They will move until the field is zero. So the electric field inside a conductor must be zero. The field inside a conductor is 0!