Download LectNotes6-Thevenin

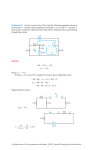
EE 215 Fundamentals of Electrical Engineering
Lecture Notes
Thévenin Equivalents
8/3/01
Rich Christie
Overview:
Along with "How many h's and f's in Kirchhoff?" (2 each), "Where does the accent go in
Thevenin?" is a leading EE trivia question. For the record it's Thévenin. His equivalent
can help simplify complicated problems, and is a powerful circuit concept.
Thevenin Equivalent:
Thevenin was a French engineer who had an idea: Take any linear circuit. Take any two
points (terminals). Pretend that the rest of the circuit is in a black box. Regardless of what
is actually in the black box, we can pretend that what is in there is a voltage source with a
resistance in series. This is called the Thevenin equivalent.
18 V
+
5A
Rt
+
3!
3!
-
vt
3!
The equivalent is mostly useful when we are concerned about one circuit element, often
representing the output of the circuit. For example, suppose the right-most 3 Ω resistor is
the circuit load. We want to know the power delivered to the load. We can compute the
Thevenin equivalent seen by the load - that is, the Thevenin equivalent of the circuit
consisting of everything except the load.
18 V
+
5A
Rt
3!
3!
+
-
vt
3!
3!
1
The process of finding a Thevenin equivalent depends on what's in the circuit.
Simple Thevenin Equivalents:
Easiest case: Independent sources and resistors:
1. Find the open circuit voltage - that's the voltage with nothing attached to the terminals.
Pretty clearly, this is the Thevenin equivalent voltage vt. In fact, people often write voc
instead of vt to help them remember. We want the terminals of the black box (the dotted
line) to be open, which means removing whatever is connected to them that is not in the
box:
18 V
+
+
voc
3!
5A
-
Now we can find voc from
superposition.
3!
-
voc = !18 + 3 " 5 = !3V
2. Find the Thevenin equivalent
resistance Rt by zeroing all the
independent sources and combining
resistances.
Rt = 3 + 3 = 6!
6!
+
-
-3V
By adding the load back in, it's easy to see that the load
voltage is 1V (OK, -1V) and the power consumed is 1/3
W.
3!
Note that the terminal voltage changes when something
is connected.
2
Try finding the Thevenin equivalent seen by the center 3 Ω resistor:
Rt = 6!
18 V
+
Voc = 18 + 5 ! 6 = 48V
3!
5A
3!
More Systematic Thevenin Equivalent:
A little harder: Independent and dependent sources, or resistors that do not combine
easily.
1. Find open circuit voltage voc the usual way.
2. Find short circuit current isc. That's current with the terminals short circuited. (This
may be dangerous in real life!)
3. Then
Rt =
voc
(and, yes, this will work for easy circuits too)
isc
Example: Here, short circuit
current is easy,
10 !
2 A 10 !
2A
10 !
4A
10 !
!
2 A 10
2A
isc = 4 A
For open circuit voltage, we
could use nodal analysis, but in
this special case we can appeal to
symmetry. The current must
evenly divide between the two
upper resistors - and between the
two lower ones, too. Then
voc = 2(10 + 10) = 40V
v
40
Rt = oc =
= 10!
isc
4
if we put a 3 ohm resistor on this circuit, the power consumption would be a bit different!
3
10 !
+
40V
-
Let's try the dependent source thing. Find the Thevenin equivalent seen by RL.
2!
5V
+
3!
(Remember to remove RL from
the circuit before taking the
equivalent!)
a
RL
vab/4
b
2!
5V
3!
a
isc
+
vab/4
Hmm, isc is probably easiest,
because vab is zero. Then
5V
isc =
= 1A
2+3
b
2!
5V
+
3!
a
vab/4
b
For voc, note that vab is also the
voltage across the dependent
current source - and the voltage
across the 2 Ω resistor will be
determined by the current source.
Then KVL around the loop is
4
vab
+ vab = 0
4
v ab = 10V = voc
v
10
Rt = oc =
= 10!
isc
1
!5!2
10 !
+
10V
-
Thevenin Equivalent with Dependent Sources:
Finally, what to do about dependent sources only. Basically, voc is zero and it's just a
matter of finding Rt. But the dependent source won't do anything unless another source is
connected to the terminals. Normally a 1A current source is used, and the terminal
voltage is found. Then
Rt =
vab
1A
Example:
-
2+vab/2
2!
1+vab/4
+
3V
-
3!
+
a
1A
vab/4
1A
b
Now we could solve this circuit
using nodal or mesh analysis, but I'll
be heuristic, and try to write
everything in terms of vab, which we
are trying to find. (This doesn't
always work!) Note that the current
through the 3 Ω resistor is 1 A, so
the voltage across it is 3V. Then the
current through the 2 Ω resistor is
1+vab/4, so the voltage across it is
2+vab/2. The voltage across the 1A
source is vab, so KVL gives
5
" vab + 3 + 2 +
vab
=0
2
vab
=5
2
vab = 10V
Rt =
10
= 10!
1
It's just the same equivalent resistance as the previous
problem with the source zeroed, which is sort of what
we expect. But voc is zero:
10 !
Note that circuits with dependent sources can give rise
to negative Thevenin equivalent resistances.
Norton Equivalent:
There's another kind of equivalent that for some reason takes second place to the
Thevenin equivalent. That's the Norton equivalent. (Heyyyyyy Norton! - any Jackie
Gleason fans in the crowd?)
Norton equivalents are current sources in parallel with a resistor: (Hint: one of these
circuits is NOT a Norton equivalent!)
Rt
in
Req
voc
+
-
Let's try to find Norton equivalent parameters in terms of Thevenin equivalent
parameters, i.e. find the Norton equivalent of the generic Thevenin equivalent.
Open circuit voltages should be equal:
6
voc = Req in
Short circuit currents should be equal
in =
voc
which is how to find the Norton current.
Rt
Subbing in
voc = Req
voc
Rt
Req = Rt
So actually the Norton is the dual of the Thevenin, it just has short circuit current instead
of open circuit voltage, and the same equivalent resistance!
So to find the Norton equivalent, you find short circuit current instead of open circuit
voltage, and then do the same things (including 1A current sources if needed) to find the
equivalent resistance. Or, find Thevenin equivalent and convert (which is longer to do but
easier to remember, so it's often what I find myself doing).
Find Norton equivalent of:
10 !
+
-
10V
1A
10!
Maximum Power Transfer:
Suppose we are designing a stereo. We made this great amplifier, and now we want to
pick speakers. It turns out that we can model a speaker (badly!) as a resistor, RL. In this
case, picking the speaker just means choosing RL. We want speakers that dissipate the
maximum power in RL, because in this case, dissipated power translates to sound output,
and we want to rock the neighborhood - like, from Seattle to Portland. So what value of
RL dissipates the maximum power?
We need to know something about the amplifier we just built. Specifically, we need to
know the Thevenin equivalent (!). So suppose we know voc and Req. Then the complete
circuit looks like:
7
OK, so
Req
2
& voc #
! R
pL = i RL = $
$R +R ! L
L "
% eq
2
voc
+
RL
-
Is the formula for the output power. How
do we find the maximum with respect to
RL?
Take derivative wrt RL and set to zero,
solve for RL. Works for any function. Any differentiable function, anyway.
(Oh, man, I thought I was done with calculus!)
dp L
RL
d
= voc2
dRL
dRL (Req + RL )2
= voc2
d
!2
RL (Req + RL )
dRL
[
]
= voc2 (1)(Req + RL ) + RL (! 2 )(Req + RL ) (1)
!2
!3
And set the derivative equal to zero
'
$
2 RL
1
voc2 %
!
=0
2
3"
(
)
(
)
R
+
R
R
+
R
L
eq
L
&% eq
#"
1!
2 RL
=0
Req + RL
2 RL = Req + RL
RL = Req !
All this math leads to a simple yet important result:
Maximum power transfer occurs when the load resistance equals the equivalent
resistance.
Turn that thing down, dude! And it works for Norton as well as Thevenin, since the
equivalent resistances are the same.
8