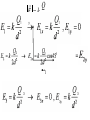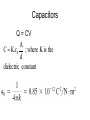* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Review 16 and 17
Electromagnetism wikipedia , lookup
Electrical resistivity and conductivity wikipedia , lookup
Speed of gravity wikipedia , lookup
Work (physics) wikipedia , lookup
Potential energy wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Magnetic monopole wikipedia , lookup
Maxwell's equations wikipedia , lookup
Field (physics) wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Lorentz force wikipedia , lookup
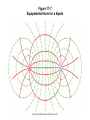
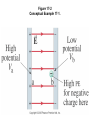
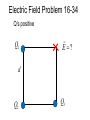
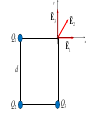
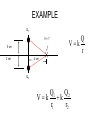
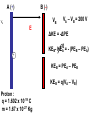
Review 16 and 17 Review • 2 kinds of charges (+, -) • Unit = Coulomb (proton, electron = ± 1.6 x 10-19 C • Like repel, opposites attract • Insulators, Conductors • Charge by rubbing, conduction, induction Two Point Charges Force : q1 q 2 F k 2 r Direction: Like charges repel, opposite charges attract q1q 2 Potential Energy : PE k r k 9 10 N m /C 9 2 2 Point Charge Surrounding a charge there is a vector field E defined at a point. q E k 2 r Direction is defined as the direction a positive test charge would move and for any other charge placed at that point : F qE Point Charge Surrounding a charge there is a scalar field V defined at a point. q Vk r and for any other charge placed at that point : PE qV How E and V related • Electric potential energy: • Electric potential difference: work done to move charge from one point to another • Relationship between potential difference and field: Figure 17-8 Topographic map Figure 17-7 Equipotential lines for a dipole Figure 17-1 Work is done by the electric field in moving the positive charge from position a to position b. Figure 17-2 Conceptual Example 17-1. Vectors • • • • Finding the resultant Force on a Charge Finding the resultant Electric Field at a point. Draw pictures with a coordinate system Always use magnitudes of the charges in the calculations • Directions determined by like repel and opposites attract (forces) or direction a small positive test charge would move (Electric Field) • Must add components separately i.e. all xcomponents first for resultant x-component. Same with y-components. Electric Field Problem 16-34 Q’s positive Q1 E ? d Q2 Q3 y E3 Q1 E2 E1 d Q2 Q3 x Q E k 2 r y 1 E3 2 1 E2 2 x E1 3 3 3y Scalars • Finding the potential energy on a charge due to other charges or finding V at a point does not require vectors. • Must use sign of charges in calculations. • Just add terms together (+ and -) EXAMPLE Q1 V=? 3 cm 3 cm Q Vk r 4 cm Q2 Q1 Q2 Vk k r1 r2 Capacitors ΔV +Q E -Q Capacitors Q = CV A C 0 ; where is the d dielectric constant Capacitors 2 Q PE 1 2 QV 1 2 CV 1 2 C PE Volume 2 1 2 0 E A (+) B (-) VB VA E VA – VB = 200 V ΔKE = -ΔPE KEB- KEA0 = - (PEB – PEA) + KEB = PEA – PEB KEB = q(VA – VB) Proton : q = 1.602 x 10-19 C m = 1.67 x 10-27 Kg