* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Magnetic field
Field (physics) wikipedia , lookup
Condensed matter physics wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Maxwell's equations wikipedia , lookup
Magnetic field wikipedia , lookup
Neutron magnetic moment wikipedia , lookup
Magnetic monopole wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Electromagnetism wikipedia , lookup
Superconductivity wikipedia , lookup
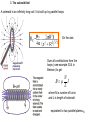
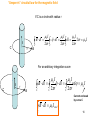
29-30 Magnetism - content Magnetic Loadspeaker •Magnetic Force – Parallel conductors •Magnetic Field •Current elements and the general magnetic force and field law •Lorentz Force •Origin of magnetic force Recording and playback unit •Application of magnetic field formula •”Amperes” circuital law •Application of the circuital law •Magnetic dipoles 1 29-30 Magnetism is the interactions between charge in motion, i.e. currents. Ampere 1820-1825 measured interactions between currents in closed conductors 2 Starting point is the parallel currents I1 I2 L r F12 0 I1 I 2 Lrˆ 2r Sign of current according to direction => •anti-parallel currents repell •parallel currents attract 3 Magnetic field F12 0 I1 I 2 Lrˆ 2r F12 I 2 L B12 B12 L in current direction 0 I1 ˆ 2r 4 Current element A current element is a vector defined as Magnified current element dt da J dl Idl J da dl nev dt qv dI = J . da 5 Magnetic field from a current element We will show that contribution from a current element is 0 I dy sin dB 4 r2 r r 2 y2 Total field in point B is then r 0 I B 4 0 I 4 For a a a dy a dy sin 0 I 2 r 4 r ( r 2 y 2 )3 / 2 a a dy r r 3 0 I 2a 4 r r 2 a 2 0 I a , B 2r 6 General magnetic force law dF12 I 2 dL2 dB12 0 I1 dy sin 0 I1 dL1 rˆ dB12 2 4 r 4 r2 dF12 Since Law of Biot-Savart 1820 0 I1I 2 dL1 rˆ dL2 4 r2 Idl J da dl nev dt qv v2 F12 0 q1q2 v1 rˆ v2 2 4 r v1 q2 r q1 7 Field Theory 8 The Hall effect A current carrying conductor in a magnetic field DV = V2-V1 = EHL = vdBL. A Hall probe can be used to ”measure” the magnetic field. L 9 (Interaction between moving free charges) Consider two electron beams: From this we conclude: R e- fe fm fm e- fe e- fe fm e - V v fe V’ v’ 1 R fe fm 3.0 108 m / s c Use 0 0 q2 v2q 2 ˆ fm R 2 2 40c R 40 R 2 fTOT Rˆ 1 q2 v2 ˆ 1 2 R 2 40 R c 1 10 (Relative motion) Electromagnetism Observer at rest V V Electric Force V Observer in motion Relative rest q1 q 2 Rˆ fe 40 R 2 1 q1q2 v 2 ˆ Magnetic Force f m R 40 R 2 c 2 0 1 0c 2 R 11 (Origin of magnetic effect – interactions take time) Assume • Interaction speed c R*=ct • Invariance of interaction speed vt v v R=ct0 R R* 2 R * R (vt) R (v ) c v2 2 R * (1 2 ) R 2 c R2 2 R* v2 1 2 c 2 2 2 2 In motion, interaction occurs over a larger distance, R*, and the strength decreases. Coulombs law changes to f em q1 q 2 Rˆ fe 40 R 2 1 q1q2 ˆ 1 q1q2 v 2 ˆ 1 2 R R 2 2 * 40 R 40 R c which is electric plus magnetic force 12 Calculations of the magnetic field 1. Field on axis from a circular current loop 0 I dL rˆ dB 4 r2 13 2. Field from an ”infinite” current plane Consider plane to consist of parallel threads of infinitesimal thickness y K is current line density (A/m) x r Q Q y From one thread 0 dI dB ˆ 2r dB 0 2 0 2 Kdy y r 2 K y r 2 2 ( 2 0 0 K 1 ˆ ˆ By Kr 2 dy y 2 2 y r 2 (sin xˆ cos yˆ ) y y r 2 2 xˆ r y r 2 2 yˆ )dy 14 3. The solenoid field A solenoid is an infinitely long coil. It is built up by parallel loops: On the axis Sum all contributions from the loops ( see example 30.4 in Benson) to get N B I L where N is number of turns and L is length of solenoid equivalent to two parallel planes15 ”Ampere’s” circuital law for the magnetic field If C is a circle with radius r I C 0 I 0 I 0 I C B dl 2r C ˆ dl 2r C dl 2r 2r 0 I I r dl For an arbitrary integration curve C I I r dl 0 I 0 I ˆ C B dl C 2r dl C 2r rd 0 I B dl I Current enclosed by curve C 0 encl C 16 Verification of Amperes circuital law 1. Current carrying plate Integration path C B dl I B 0 encl C B 2 L 0 KL I = KL B L 2. Solenoid 0 K 2 since solenoid approximation means neglecting all field outside coil L 17 Application of Circuit Law Coaxial cable with homogenous current over cross sectional area: a. Identify symmetry: cylindrical, i.e. circles around axis. b. Choose integration path as circles around axis B dl I 0 encl I 0 J da C S where S is the surface bounded by C I 1. r r1 Current density Integration path I J 2 nˆ r1 I B 2r 0 2 r 2 r1 I B 0 r 2 2r1 18 B dl I Coaxial cable with homogenous current over cross sectional area: 0 encl C S 2. I I 0 J da r2 r r1 B 2r 0 I B 0 I 2r r Integration path 19 B dl I 0 encl Coaxial cable with homogenous current over cross sectional area: C 3. S r3 r r2 Current density I I r Integration path 0 J da I J nˆ 2 2 (r3 r2 ) I 2 2 B 2r 0 I 0 ( r r 2 ) 2 2 (r3 r2 ) 0 I (r32 r22 ) (r 2 r22 ) B 2 2 2r (r3 r2 ) 0 I r32 r 2 2r (r32 r22 ) 20 B dl I 0 encl Coaxial cable with homogenous current over cross sectional area: C 4. I I 0 J da S r r3 I encl I I 0 B 0 Integration path 21 Magnetic dipoles Compare a solenoid with a permanent bar magnet A current loop is the infinitesimal magnetic dipole. What is its dipole moment? 22 Torque and energy for interacting magnetic dipole Torque is Magnetic dipole moment is defined so that and vectorially t B Energy Work to rotate from aligned to anti-aligned is So that magnetic energy is U m B Equivialent with electric dipole 23 formulas. (Minus sign is conventional, but not correct) Earth Magnetism 24 Magnetism in Biology Magnetite found in animals Solomon fish Bacteria Pigeon bird 25