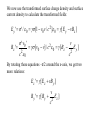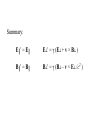Download Lecture3

Ben Gurion University of the Negev
www.bgu.ac.il/atomchip, www.bgu.ac.il/nanocenter
Physics 3 for Electrical Engineering
Lecturers: Daniel Rohrlich, Ron Folman
Teaching Assistants: Daniel Ariad, Barukh Dolgin
Week 3. Special relativity – transformation of the E and B fields •
the field tensor Fmn • electromagnetic field of a charge moving at
constant velocity
Sources: Feynman Lectures II, Chap. 13 Sect. 6, Chap. 25, and
Chap. 26, Sects. 2-3;
E. M. Purcell, Electricity and Magnetism, Berkeley Physics Course
Vol. 2, Second Edition, 1985, Sect. 6.7
Transformation of the E and B fields
Now that we have derived the relativistic transformation
laws for space, time, velocity, momentum and energy,
let’s look for the transformation laws for E and B.
These fields are determined by Maxwell’s equations, and
Maxwell’s equations already obey Einstein’s postulate
that the speed of light is a universal constant. Hence the
relativistic transformation laws for E and B should not
present any problem. But how do we discover them?
Transformation of the E and B fields
Now that we have derived the relativistic transformation
laws for space, time, velocity, momentum and energy,
let’s look for the transformation laws for E and B.
These fields are determined by Maxwell’s equations, and
Maxwell’s equations already obey Einstein’s postulate
that the speed of light is a universal constant. Hence the
relativistic transformation laws for E and B should not
present any problem. But how do we discover them?
No progress without a paradox!
– John A. Wheeler
A paradox:
I→
B
FL
v
A current I = ρ– A v runs in a straight wire, where A is the
cross-sectional area of the wire and ρ– < 0 is the
(negative) charge density of the electrons. A particle of
negative charge q moves parallel to the wire, with the
same velocity v. Since the charged particle moves in the
magnetic field of the current, it feels the Lorentz force
FL = q v × B
.
A paradox:
I→
B
But in the rest frame of the particle, it feels no Lorentz
force!
A paradox:
I→
B
FC = 0
v
Let’s go back to the rest frame of the wire. Let ρ+ > 0
denote the (positive) charge density of the protons. We
will assume |ρ–| = ρ+ and therefore there is no Coulomb
force FC in this frame.
A paradox:
I→
B
FL
v
Calculation: in the rest frame of the wire, the field is
B = I / 2π rc2ε0 = ρ+ A v / 2π rc2ε0 , where r is the distance
from the charged particle to the axis of the wire. Thus the
Lorentz force is
FL = qvB = qρ+ A v2 / 2π rc2ε0 .
A paradox:
I→
B
FC'
In the rest frame of the particle, there is no Lorentz force,
but there is instead a Coulomb force due to unbalanced
charge concentrations ρ+' > 0 and ρ–' < 0:
 '
  '

   
.

A paradox:
I→
B
FC'
In the rest frame of the particle, there is no Lorentz force,
but there is instead a Coulomb force of magnitude

FC '  (  
)


 4πε0 (r 2  x 2 )
q
r
r 2  x2
Adx

 q A q Av 2
1


 1 v2 / c2 
 

 2πε0 r 2π rc 2 ε
2
2
0
 1 v / c

.
A paradox:
I→
B
FC'
Actually, what has to be equal is not FL and FC' but the
change in transverse momentum FLΔt and FC'Δt'. Since
Δt = γΔt‘ we indeed find
2  q A

t 
1  q  A
2
2

   
FC ' t ' 
 t 1  1  v / c 

 2πε r
 
  2πε0 r
0


 q  Av 2 t / 2π rc 2 ε0  FL t .
We have learned an important lesson: If we want
to understand how E and B transform from one
inertial reference frame to another, we should
look at how the charge and current densities
transform.
K
So let’s consider two
infinite, parallel sheets
of uniform surface
charge densities σ and –σ
(as measured in the
inertial frame K),
moving with speed v0 in
the positive x-direction.
We have Ex = 0 = Ez while
Ey = σ/ε0 and Bx = 0 = By
while Bz = σ v0/c2ε0
(between the parallel
sheets).
v
K′
K
Now in an inertial frame K′, moving with speed v in the positive
x-direction relative to K, the speed of the sheets v0′ is
v0 ' 
v0  v
1  v0v / c 2
v
K′
K
In K′ the magnitude of the surface charge density is σ′ = σ γ0′/γ0
= σ γ(1 – v0v/c2 ), where
0 
1
1  (v0 / c) 2
,  0'
1
1  (v0 ' / c) 2
, 
1
1  (v / c ) 2
Some algebra:
 0'




1
1  (v0 ' / c) 2
1
2
 0   

1  
 1  0 
1  0
(1   0  ) 2   0   2
1  0

1  2 0    0 2  2   0 2   2  2 0 
1  0
1   1   
2
0
2
  0 (1   0  )

v
K′
K
In K′ the surface charge density is σ′ = σ γ(1 – v0v/c2 ) and the
surface current density is σ′v0′ which is
 ' v0 '   (1  v0v / c )
2
v0  v
1  vv0 / c
2
  (v0  v)
We now use the transformed surface charge density and surface
current density to calculate the transformed fields:
E y '   ' /  0   [1  v0 v / c 2 ] 0   [ E y  vBz ]
Bz ' 
 ' v0 '
c 0
2
  [v0  v] / c  0   [ Bz 
2
v
c
2
Ey ]
By rotating these equations –π/2 around the x-axis, we get two
more relations:
E z '   [ E z  vB y ]
v
By '   [By  2 Ez ]
c
Finally, the components of E and B parallel to the boost axis do
not change:
Ex '  Ex
Bx '  Bx
How do we know? A boost perpendicular to the plates only
changes the separation of the plates – that does not change the
electric field. A boost along the axis of a solenoid multiplies
the density of the wires around the solenoid by a factor γ but
reduces the current in each by a factor of γ (time dilation) so it
does not change the magnetic field.
Summary:
E║′ = E║
E┴′ = γ (E┴ + v × B┴ )
B║′ = B║
B┴′ = γ (B┴ – v × E┴ /c2 )
The field tensor Fmn
(Here we take c = 1.) We can write the electromagnetic
field as a tensor F:
0
E
x
F
E y

 E z
 Ex
0
Bz
 By
 Ey
 Bz
0
Bx
 Ez 
B y 
 Bx 

0 
If L is any Lorentz transformation in matrix form, then
F’ = LFLT.
For example, if L is
 

  
L
0

 0

 
0 0

0 0
1 0

0 1 

0
0
then F’ is
 

  
F'  
0

 0

 

0
0
0
0
1
0
0  0

0  E x
0  E y

1  E z
 Ex
0
Bz
 By
 Ey
 Bz
0
Bx
 Ez   

B y    
 Bx   0

0   0
 

0
0
0
0
1
0
0

0
0

1 
Electromagnetic field of a charge moving at constant velocity
The field of an electric charge in its rest frame is
E
q
4 0 r
ˆ
r
2
;
if we boost it to a frame K′ moving in the positive x-direction,
it is the electromagnetic field of a charge moving at constant v.
[J. D. Jackson, Classical Electrodynamics, Sect. 11.10:]
Consider an observer at the point P = (0,b,0) in the frame K:
y
y′
x′
x
z
z′
The origins coincide at time t = 0 = t′.
Coordinates of P in reference frame K′: (–vt′,b,0)
Distance of P from charge:
r '  b 2  (vt ' ) 2  b 2  v 2 2 (t  vx / c 2 ) 2  b 2  v 2 2t 2
Components of E′: E x ' 
qvt'
4 0 (r ' )
3
, Ey '
qb
4 0 (r ' )
Components of B′: B′ = 0
y
y′
x′
x
z
z′
3
, Ez '  0
The nonvanishing field components in K′ are
Ex '  

qv t
4 0 b  v  t
2

and in K they are E x  E x '  
E y  E y ' 
, Ey '
2 2 2 3/ 2



qb
4 0 b  v  t
qv t

2 2 2 3/ 2
4 0 b 2  v  t
q b

2 2 2 3/ 2
4 0 b 2  v  t
y
, Bz 
vE y '
c
y′
x′
x
z
z′

2 2 2 3/ 2
2
2
,

v
c
2
Ey
We can also freeze t and vary b to map out the field at a
given time t. From the figure we see that
r sin ψ = b ,
which allows us to write E 
r cos ψ = –vt ,
qrˆ
4 0 r 2 2 (1   2 sin 2 ψ)3 / 2
y
y′
x′
x
z
z′
Lines of force for E 
qrˆ
4 0 r 2 2 (1   2 sin 2 ψ)3 / 2
v
v=0