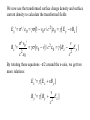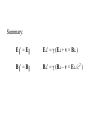* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture3
Eddy current wikipedia , lookup
Hall effect wikipedia , lookup
Abraham–Minkowski controversy wikipedia , lookup
Magnetic monopole wikipedia , lookup
Static electricity wikipedia , lookup
Electromotive force wikipedia , lookup
Electricity wikipedia , lookup
Computational electromagnetics wikipedia , lookup
Electric charge wikipedia , lookup
Maxwell's equations wikipedia , lookup
Electrostatics wikipedia , lookup
Faraday paradox wikipedia , lookup
Electromagnetic field wikipedia , lookup
Ben Gurion University of the Negev www.bgu.ac.il/atomchip, www.bgu.ac.il/nanocenter Physics 3 for Electrical Engineering Lecturers: Daniel Rohrlich, Ron Folman Teaching Assistants: Daniel Ariad, Barukh Dolgin Week 3. Special relativity – transformation of the E and B fields • the field tensor Fmn • electromagnetic field of a charge moving at constant velocity Sources: Feynman Lectures II, Chap. 13 Sect. 6, Chap. 25, and Chap. 26, Sects. 2-3; E. M. Purcell, Electricity and Magnetism, Berkeley Physics Course Vol. 2, Second Edition, 1985, Sect. 6.7 Transformation of the E and B fields Now that we have derived the relativistic transformation laws for space, time, velocity, momentum and energy, let’s look for the transformation laws for E and B. These fields are determined by Maxwell’s equations, and Maxwell’s equations already obey Einstein’s postulate that the speed of light is a universal constant. Hence the relativistic transformation laws for E and B should not present any problem. But how do we discover them? Transformation of the E and B fields Now that we have derived the relativistic transformation laws for space, time, velocity, momentum and energy, let’s look for the transformation laws for E and B. These fields are determined by Maxwell’s equations, and Maxwell’s equations already obey Einstein’s postulate that the speed of light is a universal constant. Hence the relativistic transformation laws for E and B should not present any problem. But how do we discover them? No progress without a paradox! – John A. Wheeler A paradox: I→ B FL v A current I = ρ– A v runs in a straight wire, where A is the cross-sectional area of the wire and ρ– < 0 is the (negative) charge density of the electrons. A particle of negative charge q moves parallel to the wire, with the same velocity v. Since the charged particle moves in the magnetic field of the current, it feels the Lorentz force FL = q v × B . A paradox: I→ B But in the rest frame of the particle, it feels no Lorentz force! A paradox: I→ B FC = 0 v Let’s go back to the rest frame of the wire. Let ρ+ > 0 denote the (positive) charge density of the protons. We will assume |ρ–| = ρ+ and therefore there is no Coulomb force FC in this frame. A paradox: I→ B FL v Calculation: in the rest frame of the wire, the field is B = I / 2π rc2ε0 = ρ+ A v / 2π rc2ε0 , where r is the distance from the charged particle to the axis of the wire. Thus the Lorentz force is FL = qvB = qρ+ A v2 / 2π rc2ε0 . A paradox: I→ B FC' In the rest frame of the particle, there is no Lorentz force, but there is instead a Coulomb force due to unbalanced charge concentrations ρ+' > 0 and ρ–' < 0: ' ' . A paradox: I→ B FC' In the rest frame of the particle, there is no Lorentz force, but there is instead a Coulomb force of magnitude FC ' ( ) 4πε0 (r 2 x 2 ) q r r 2 x2 Adx q A q Av 2 1 1 v2 / c2 2πε0 r 2π rc 2 ε 2 2 0 1 v / c . A paradox: I→ B FC' Actually, what has to be equal is not FL and FC' but the change in transverse momentum FLΔt and FC'Δt'. Since Δt = γΔt‘ we indeed find 2 q A t 1 q A 2 2 FC ' t ' t 1 1 v / c 2πε r 2πε0 r 0 q Av 2 t / 2π rc 2 ε0 FL t . We have learned an important lesson: If we want to understand how E and B transform from one inertial reference frame to another, we should look at how the charge and current densities transform. K So let’s consider two infinite, parallel sheets of uniform surface charge densities σ and –σ (as measured in the inertial frame K), moving with speed v0 in the positive x-direction. We have Ex = 0 = Ez while Ey = σ/ε0 and Bx = 0 = By while Bz = σ v0/c2ε0 (between the parallel sheets). v K′ K Now in an inertial frame K′, moving with speed v in the positive x-direction relative to K, the speed of the sheets v0′ is v0 ' v0 v 1 v0v / c 2 v K′ K In K′ the magnitude of the surface charge density is σ′ = σ γ0′/γ0 = σ γ(1 – v0v/c2 ), where 0 1 1 (v0 / c) 2 , 0' 1 1 (v0 ' / c) 2 , 1 1 (v / c ) 2 Some algebra: 0' 1 1 (v0 ' / c) 2 1 2 0 1 1 0 1 0 (1 0 ) 2 0 2 1 0 1 2 0 0 2 2 0 2 2 2 0 1 0 1 1 2 0 2 0 (1 0 ) v K′ K In K′ the surface charge density is σ′ = σ γ(1 – v0v/c2 ) and the surface current density is σ′v0′ which is ' v0 ' (1 v0v / c ) 2 v0 v 1 vv0 / c 2 (v0 v) We now use the transformed surface charge density and surface current density to calculate the transformed fields: E y ' ' / 0 [1 v0 v / c 2 ] 0 [ E y vBz ] Bz ' ' v0 ' c 0 2 [v0 v] / c 0 [ Bz 2 v c 2 Ey ] By rotating these equations –π/2 around the x-axis, we get two more relations: E z ' [ E z vB y ] v By ' [By 2 Ez ] c Finally, the components of E and B parallel to the boost axis do not change: Ex ' Ex Bx ' Bx How do we know? A boost perpendicular to the plates only changes the separation of the plates – that does not change the electric field. A boost along the axis of a solenoid multiplies the density of the wires around the solenoid by a factor γ but reduces the current in each by a factor of γ (time dilation) so it does not change the magnetic field. Summary: E║′ = E║ E┴′ = γ (E┴ + v × B┴ ) B║′ = B║ B┴′ = γ (B┴ – v × E┴ /c2 ) The field tensor Fmn (Here we take c = 1.) We can write the electromagnetic field as a tensor F: 0 E x F E y E z Ex 0 Bz By Ey Bz 0 Bx Ez B y Bx 0 If L is any Lorentz transformation in matrix form, then F’ = LFLT. For example, if L is L 0 0 0 0 0 0 1 0 0 1 0 0 then F’ is F' 0 0 0 0 0 0 1 0 0 0 0 E x 0 E y 1 E z Ex 0 Bz By Ey Bz 0 Bx Ez B y Bx 0 0 0 0 0 0 0 1 0 0 0 0 1 Electromagnetic field of a charge moving at constant velocity The field of an electric charge in its rest frame is E q 4 0 r ˆ r 2 ; if we boost it to a frame K′ moving in the positive x-direction, it is the electromagnetic field of a charge moving at constant v. [J. D. Jackson, Classical Electrodynamics, Sect. 11.10:] Consider an observer at the point P = (0,b,0) in the frame K: y y′ x′ x z z′ The origins coincide at time t = 0 = t′. Coordinates of P in reference frame K′: (–vt′,b,0) Distance of P from charge: r ' b 2 (vt ' ) 2 b 2 v 2 2 (t vx / c 2 ) 2 b 2 v 2 2t 2 Components of E′: E x ' qvt' 4 0 (r ' ) 3 , Ey ' qb 4 0 (r ' ) Components of B′: B′ = 0 y y′ x′ x z z′ 3 , Ez ' 0 The nonvanishing field components in K′ are Ex ' qv t 4 0 b v t 2 and in K they are E x E x ' E y E y ' , Ey ' 2 2 2 3/ 2 qb 4 0 b v t qv t 2 2 2 3/ 2 4 0 b 2 v t q b 2 2 2 3/ 2 4 0 b 2 v t y , Bz vE y ' c y′ x′ x z z′ 2 2 2 3/ 2 2 2 , v c 2 Ey We can also freeze t and vary b to map out the field at a given time t. From the figure we see that r sin ψ = b , which allows us to write E r cos ψ = –vt , qrˆ 4 0 r 2 2 (1 2 sin 2 ψ)3 / 2 y y′ x′ x z z′ Lines of force for E qrˆ 4 0 r 2 2 (1 2 sin 2 ψ)3 / 2 v v=0