* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download PowerPoint
Anti-gravity wikipedia , lookup
Condensed matter physics wikipedia , lookup
Electromagnetism wikipedia , lookup
Circular dichroism wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Lorentz force wikipedia , lookup
Potential energy wikipedia , lookup
Maxwell's equations wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Chien-Shiung Wu wikipedia , lookup
Field (physics) wikipedia , lookup
Electric charge wikipedia , lookup
Time in physics wikipedia , lookup
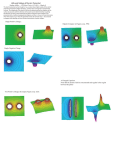
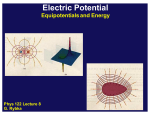
Physics 212 Lecture 6 Today's Concept: Electric Potential Defined in terms of Path Integral of Electric Field Physics 212 Lecture 6, Slide 1 Music Who is the Artist? A) B) C) D) E) John Prine Little Feat Taj Mahal Ry Cooder Los Lobos Why? Last time did Buena Vista Social Club (Cuba) Ry Cooder was the guy who brought them to our attention in this country Also, this album is great…. NOTE: Ellnora starts tonight….. Physics 212 Lecture 6 Your Comments “I'm pretty sure my head just exploded. Just... everywhere.” “help! i need somebody help! not just anybody help! you know i need someone HELLPP" “That last one was a doozy. Equipotential lines seem like they hold the key to something, but I don't know what yet.” Electric potential is related to energy – a key aspect of E’nM. We will use electric potential extensively when we talk about circuits. “Do we have to be able to use/do problems with gradients?” “Are we going to differentiate the electric potential in three dimensions in order to get the electric field?” We really only need to know about derivatives (partial derivatives in a few cases). “The calculations with the spherical insulator were hard to follow. And I understand simple ideas, but I hope that the lecture helps me understand more fully.” See example at end of class. Not too bad. After discussion today, I understand Gauss's Law! 05 Physics 212 Lecture 6, Slide 3 BIG IDEA • Last time we defined the electric potential energy of charge q in an electric field: b F dl qE dl b U ab a a •The only mention of the particle was through its charge q. • We can obtain a new quantity, the electric potential, which is a PROPERTY OF THE SPACE, as the potential energy per unit charge. Vab b U ab E dl q a •Note the similarity to the definition of another quantity which is also a PROPERTY OF THE SPACE, the electric field. F E q 40 Physics 212 Lecture 6, Slide 4 Electric Potential from E field • Consider the three points A, B, and C located in a region of constant electric field as shown. D x • What is the sign of VAC = VC - VA ? (A) VAC < 0 (B) VAC = 0 • Remember the definition: VAC (C) VAC > 0 C E dl A • Choose a path (any will do!) C E dl E dl D VAC A 40 D 0 E dl Ex 0 C VAC D Physics 212 Lecture 6, Slide 5 Checkpoint 2 Suppose the electric field is zero in a certain region of space. Which of the following statements best describes the electric potential in this region of space? A A. The B electric potential is zero everywhere in this region B. The electric potential is zero at at least one point in this region C. The D electric potential is constant everywhere in this region D. There is not enough information to distinguish which of the answers is correct When you integrate 0, you get 0, everywhere. When the electric field is zero in a certain region, the electric potential is surely zero in that region. However it is not certain that the electric potential is zero elsewhere. The potential is the integral of E dx. If E is zero then when you integrate you will just get a constant. • Remember the definition E dl B VA B E 0 08 A VAB 0 V is constant !! Physics 212 Lecture 6, Slide 6 E from V • If we can get the potential by integrating the electric field: E dl b Vab a • We should be able to get the electric field by differentiating the potential?? E V • In Cartesian coordinates: Ex V x Ey V y V Ez z 40 Physics 212 Lecture 6, Slide 7 Checkpoint 1a The electric potential in a certain region is plotted in the following graph: At which point is the magnitude of the E-field greatest? A. B. C. D. “The highest electric potential also means the greatest electric field.“ “The slope is the steepest there“ “The field and the potential are inversely related“ • How do we get E from V?? E V 08 Ex = - V x Look at slopes !!! Physics 212 Lecture 6, Slide 8 Checkpoint 1b The electric potential in a certain region is plotted in the following graph: A B C D At which point is the direction of the E-field along the negative x-axis? A. B. C. D. “Because B is along the negative slope on the graph.“ “The slope of the electric potential at point C is positive“ • How do we get E from V?? E V 08 Ex = - V x Look at slopes !!! Physics 212 Lecture 6, Slide 9 Equipotentials • Equipotentials are the locus of points having the same potential Equipotentials produced by a point charge Equipotentials are ALWAYS perpendicular to the electric field lines The SPACING of the equipotentials indicates The STRENGTH of the electric field 40 Physics 212 Lecture 6, Slide 10 Checkpoint 3a The field-line representation of the E-field in a certain region of space is shown below. The dashed lines represent equipotential lines. A B C D At which point in space is the E-field weakest? A. B. C. D. “The field lines are dense at points A, B, and C, which indicates that the field is strong. However the lines are very spread out at D, indicating that the field is weakest there..“ 08 Physics 212 Lecture 6, Slide 11 Checkpoint 3b The field-line representation of the E-field in a certain region of space is shown below. The dashed lines represent equipotential lines. A B C D Compare the work done moving a negative charge from A to B and from C to D. Which move requires more work? A B A. From A to B B. From C to D C C. The same D. Cannot determine without performing calculation D “The equipotential is weaker in the region between c and d than in the region from a to b.“ “The work is directly proportional to the distance between two charges. The distance between C and D is further away from that of A and B.” “The charge would have to cross the same number of equipotential lines regardless, so the change 08 potential energy is the same and therefore the work is the same.“ in Physics 212 Lecture 6, Slide 12 HINT The field-line representation of the E-field in a certain region of space is shown below. The dashed lines represent equipotential lines. A B C D What are these ? ELECTRIC FIELD LINES !! What are these ? EQUIPOTENTIALS !! • What is the sign of WAC = work done by E field to move negative charge from A to C ? (A) WAC < 0 (B) WAC = 0 (C) WAC > 0 A and C are on the same equipotential 08 Equipotentials are perpendicular to the E field: No work is done along an equipotential WAC = 0 !! Physics 212 Lecture 6, Slide 13 Checkpoint 3b Again? The field-line representation of the E-field in a certain region of space is shown below. The dashed lines represent equipotential lines. A B C D Compare the work done moving a negative charge from A to B and from C to D. Which move requires more work? A B A. From A to B B. From C to D C C. The same D. Cannot determine without performing calculation D • A and C are on the same equipotential • B and D are on the same equipotential • Therefore the potential difference between A and B is the SAME as the potential between C and D 08 Physics 212 Lecture 6, Slide 14 Checkpoint 3c The field-line representation of the E-field in a certain region of space is shown below. The dashed lines represent equipotential lines. A B C D Now compare the work done moving a negative charge from A to B and from A to D. Which move requires more work? A B From A to B A. B. From A to D C C. D. Cannot determine without performing calculation D The same “because the electric field is constant, moving the charge from A to D would require the most work since it has the furthest displacement.” “The electric field is greater at point D than B.“ “B and D are on the same equipotential line.“ 08 Physics 212 Lecture 6, Slide 15 Calculation for Potential cross-section a4 a3 +Q a2 a1 +q Point charge q at center of concentric conducting spherical shells of radii a1, a2, a3, and a4. The inner shell is uncharged, but the outer shell carries charge Q. What is V as a function of r? metal metal • Conceptual Analysis: – – Charges q and Q will create an E field throughout space r V (r ) E d r0 • Strategic Analysis: – – 40 Spherical symmetry: Use Gauss’ Law to calculate E everywhere Integrate E to get V Physics 212 Lecture 6, Slide 16 Calculation: Quantitative Analysis cross-section a4 a3 r > a4 : What is E(r)? +Q a2 a1 1 Qq 1 Q (B) (C) 2 r 4 r (A) 0 2 +q 1 Qq 1 Qq (D) (E) 4 r 4 r metal r 2 metal Why? Gauss’ law: 0 0 E dA 0 0 Q enclosed 0 E 4 r 2 2 Qq 0 1 Qq E 4 r 2 0 Physics 212 Lecture 6, Slide 17 Calculation: Quantitative Analysis cross-section a4 a3 a3 < r < a4 : What is E(r)? +Q a2 a1 (A) 0 (B) +q metal 1 q 4 r 2 0 r 1 q (D) 4 r 2 0 metal (C) 1 q 2 r 0 1 Qq (E) 4 r 2 0 Applying Gauss’ law, what is Qenclosed for red sphere shown? (B) –q (A) q (C) 0 How is this possible??? -q must be induced at r=a3 surface 3 q 4 a 2 3 charge at r=a4 surface = Q+q 4 Qq 4 a 2 4 Physics 212 Lecture 6, Slide 18 Calculation: Quantitative Analysis cross-section a4 a3 +Q a2 a1 Continue on in…. a2 < r < a3 : E 1 q 4 r 2 0 a1 < r < a2 : +q metal r r < a1 : E 0 E 1 q 4 r 2 0 metal To find V: 1) Choose r0 such that V(r0) = 0 2) Integrate !! r > a4 : V (usual: r0 = infinity) 1 Qq 4 r 0 a3 < r < a4 : (A) V 0 (B) V (C) 1 Qq V ( a4 ) 0 4 a 1 Qq V 4 a 0 4 0 3 Physics 212 Lecture 6, Slide 19 Calculation: Quantitative Analysis cross-section a4 a3 r > a4 : +Q V 1 Qq 4 r 0 a2 a1 a3 < r < a4 : V 1 Q q 4 +q 0 a 4 metal metal a2 < r < a3 : V (r ) V ( a ) 0 V (a r ) 4 V (r ) Qq q 1 1 0 4 a 4 r a 0 a1 < r < a2 : V (r ) 3 4 0 V (r ) 3 1 Qq q q 4 a r a 0 4 3 1 Qq q q 4 a a a 0 4 2 3 1 Qq q q q q 0 < r < a1 : V (r ) 4 a a a r a 0 4 2 3 1 Physics 212 Lecture 6, Slide 20 Summary V 0 E dl b Vab a E V a1a2 a3a4 r