Download AC Circuits - San Jose State University

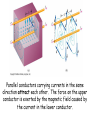
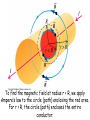
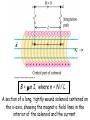
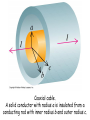
Source of Magnetic Field Ch. 28
Magnetic field of a moving charge
B field of current element
B field of current-carrying wire
Force between conductors
B field of circular current loop
Ampere’s Law
Applications of Ampere’s Law
C 2009 J. Becker
(sec. 28.1)
(sec. 28.2)
(sec. 28.3)
(sec. 28.4)
(sec. 28.5)
(sec. 28.6)
(sec. 28.7)
(a) Magnetic field vectors caused by a moving positive
point charge. At each point, B is perpendicular to the
plane containing r and v.
(b) Here the charge is moving into the screen.
Electric and magnetic
forces on one of a
pair of protons
moving in E and B
fields.
(a) Magnetic field vectors caused by current element dl.
(b) In figure (b) the current is moving into the screen.
xo
Magnetic field
produced by a
straight currentcarrying wire of
length 2a. The
direction of B at
point P is into the
screen.
Law of Biot and Savart
dB = [mo / 4p ] [(I dL x r) /
3
r ]
Magnetic field around a long, straight conductor. The
field lines are circles, with directions determined by
the right-hand rule.
Parallel conductors carrying currents in the same
direction attract each other. The force on the upper
conductor is exerted by the magnetic field caused by
the current in the lower conductor.
Use Law of Biot and Savart, the integral is simple!
dB = mo / 4p (I dL x r) /
3
r
Magnetic field caused by a circular loop of current. The
current in the segment dL causes the field dB, which
lies in the xy plane.
Ampere’s Law
Ampere’s Law states that the integral of B around
any closed path equals mo times the current, Iencircled,
encircled by the closed loop.
We will use this law to obtain some useful results by
choosing a simple path along which the magnitude of B is
constant, (or independent of dl). That way, after taking
the dot product, we can factor out |B| from under the
integral sign and the integral will be very easy to do.
See list of important results in the
Summary of Ch. 28 on p. 1094
Some (Ampere’s Law) integration paths for the line
integral of B in the vicinity of a long straight conductor.
Path in (c) is not useful because it does not encircle the
current-carrying conductor.
To find the magnetic field at radius r < R, we apply
Ampere’s law to the circle (path) enclosing the red area.
For r > R, the circle (path) encloses the entire
conductor.
xo
>
B = mon I, where n = N / L
A section of a long, tightly wound solenoid centered on
the x-axis, showing the magnetic field lines in the
interior of the solenoid and the current.
Coaxial cable.
A solid conductor with radius a is insulated from a
conducting rod with inner radius b and outer radius c.
Review
See www.physics.edu/becker/physics51
C 2009J. Becker