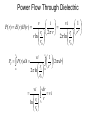Download Co-Axial Cable Analysis - Prescott Campus, Arizona

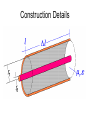
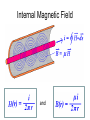
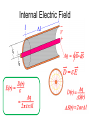
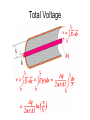
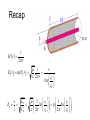
Co-Axial Cable Analysis
Construction Details
Question 1
What is the fundamental equation relating
the magnetic field surrounding a conductor
and the current in the conductor?
Ampere’s Law:
i   H  dS
Internal Magnetic Field
and
Question 2
By what method is the total flux passing
through a given area computed?
   B  dA
A
Total Flux in Short Section
Definition of
inductance:
Ratio of total flux to total linked
current causing the flux.
Incremental Inductance:
Inductance per Unit Length
Question 3
What is the fundamental equation relating
the electric field surrounding a charged
body and the charge on that body?
Gauss’s Law:
q 
 D  dA
A
Internal Electric Field
Question 4
What is the fundamental equation relating
the electric field in the region about two
bodies and the potential difference
(voltage) between those two bodies?
a
vba   E  dS
b
Total Voltage
E Field Relation to Voltage
We showed previously that:
..and since...
..therefore...
Definition of
capacitance:
Ratio of total charge to the voltage
resulting from the charge.
Incremental Capacitance
Capacitance per Unit Length
Question 5
What is the fundamental relationship
between the magnitudes of Electric and
Magnetic fields when Energy is
propagating through a medium?
Ohm’s Law
E  H
where



is the intrinsic
impedance of the
dielectric material
Induced Co-ax Voltage
We previously determined that the magnetic field
strength associated with a current in the co-ax is
given by:
H (r ) 
i
2r , thus

E (r ) 
2 r 
i
..and the voltage between inner and outer
conductor will be:
Characteristic Impedance
We see now that the ratio of voltage to current associated
with energy propagating in a coaxial cable is:
.. but, from our previous
discussion of inductance and
capacitance per unit length,
  r1 
ln  
2
2  r0    1  r1  
L0
2

 
ln     Z 0
2
C0
  2  r0  
 r1 
ln  
 r0 
L0
v
Z0  
i
C0
Recap
H r  
i
2 r
 i
E r  H r  

 2 r
L0
v
Z0  

i
C0


v
 r1 
r ln  
 r0 
 1  r1  
 1  r1  
ln      
ln   

 2  r0  
 2  r0  
Question 6
What is the fundamental equation relating
the Power density flowing through a region
and the fields in that region?
  
P  EH
Power Transfer
The Poynting Vector is used to represent the
power transferred by electromagnetic fields:
  
P  EH
If the fields are perpendicular, as
they are in this case, then
 i 
Pr   E r H r   

 2r 
2


in watts per square meter
Question 7
How do we compute the total power flowing
through a surface if we know the power
density at all points on that surface?
r1
PT   Pr dA
r0
Power Transfer (cont)
To find the total power
transfer (watts) we must
integrate P(r) over the
entire cross section of
the dielectric, between r0
and r1. . .
We’ll integrate using a ring of
thickness dr
...

u i   1
u i2
PT 
    2 2rdr  
  2  r0 r
 2

PT  i 2 Z 0  iv
2 r1
dr 2  1
r r  i  2

0
r1
  r1 
ln  
  r0 
Power Flow Through Dielectric
v
 i
P(r )  E (r ) H (r ) 

 r1   2
r ln  
 r0 
r1
r1


r
vi
1
 2
 r1   r 
2 ln  
 r0 
vi
1
PT   P(r )dA 
 2 2rdr 

 r1  r0  r 
r0
2 ln  
 r0 
r1
vi
dr

 vi

 r1  r0 r
ln  
 r0 
Traveling Waves
If one applies Kirchhoff’s Laws to a differential length of transmission
line having Inductance and Capacitance per unit length of L0 and C0
respectively, and excited by a source with radian frequency w, solution
of the resulting differential equations yields a solution for the voltage
function of the form:
j   wt   x 
V  t , x   Vi e
Vi represents a complex amplitude.
The + preceding the w t term indicates that solutions will exist in complex
conjugates to yield a real valued time function. As per our long standing
convention, we will only explicitly carry the + term through our
derivations.
The + preceding the x term indicates solutions exist representing waves
traveling in the positive and negative directions. Let’s see how this
works.
Traveling Waves (cont)
Consider the solution having the phase term (wt-x). This represents
the instantaneous phase of the voltage function.
Now consider The waveform peaks, where the instantaneous phase
equals 2N (or any point of constant phase). If we solve for x, we get
2 N
wt
2 w
xN 

N
 t


 
Two important observations can be made.
1. The distance between adjacent peaks (wavelength) is
2. The position of the peaks is increasing at a velocity
vp 

2


vp
f
w
1
1



L0C0
