* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Issues in Inflationary and Cyclic Cosmology
Path integral formulation wikipedia , lookup
Inverse problem wikipedia , lookup
Perturbation theory wikipedia , lookup
Natural computing wikipedia , lookup
Mathematical physics wikipedia , lookup
Uncertainty principle wikipedia , lookup
Renormalization wikipedia , lookup
Computational complexity theory wikipedia , lookup
Scalar field theory wikipedia , lookup
Renormalization group wikipedia , lookup
Quantum computing wikipedia , lookup
Quantum key distribution wikipedia , lookup
Maximum entropy thermodynamics wikipedia , lookup
Quantum machine learning wikipedia , lookup
Post-quantum cryptography wikipedia , lookup
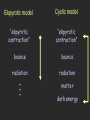
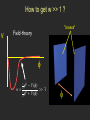
Great explanatory power: horizon – flatness – monopoles – entropy Great predictive power: ? ? ? Wtotal = 1 nearly scale-invariant perturbations slightly red tilt adiabatic gaussian gravitational waves consistency relations “the classic(al) perspective” dominantly a classical process… an ordering process… in which quantum physics plays a small but important perturbative role “the (true) quantum perspective” Inflation is dominantly a quantum process… in which (classical) inflation amplifies rare quantum fluctuations… resulting in a peculiar kind of disorder Eternal Inflation Vilenkin, 1983 PJS, 1983 “I would argue that once one accepts eternal inflation as a logical possibility, then there is no contest in comparing an eternally inflating version of inflation with any theory that is not eternal....” Alan Guth, 2000 • Powerfully predictive? Linde, Linde, Mezhlumian, PRD 50, 2456 (1994) • If Eternal to the Past, then maybe we can uniquely determine the probabilities. SINGULARITY PROBLEM cf. Borde and Vilenkin, PRL 72, 3305 (1994); PRD 56, 717 (1997) • Maybe can find measure that does not depend on initial conditions Global vs. Local Measures? • Immune from initial conditions? • Important properties insensitive to initial conditions? Garriga, Guth and Vilenkin, hep-th/0612242 Aguirre, Johnson and Shomer, arxiv:0704.3473 Chang, Kleban, Levi, arxiv:07012.2261 Aguirre, Johnson, arxiv:0712.3038 “Persistence of Memory Effect” tinitial • Important properties insensitive to initial conditions? YELLOW: anisotropic! t=0 • Perhaps we know the Iniitial Condiions?? Entropy Problem: requires entropically disfavored initial state? Penrose “the (true) quantum perspective” • Singularity problem theory incomplete ? • Unpredictability problem threatens flatness and scale invariance? • Persistence of memory threatens isotropy? • Entropy problem advantage problem “the (true) quantum perspective” • Singularity problem • Unpredictability problem • Persistence of memory 1) Inflation is fast energy density large or Hsmoothing > Hnormal >> Htoday • Entropy problem 2) Quantum physics is random “the (true) quantum perspective” • Singularity problem • Unpredictability problem • Persistence of memory • Entropy problem But suppose Hsmoothing << Hnormal How do we go from small H to large H ? H = 4 G ( p) Hsmoothing contracting implies must resolve singularity problem Ekpyrotic model Cyclic model “ekpyrotic contraction” “ekpyrotic contraction” bounce bounce radiation radiation .. . matter dark energy ekpyrotic phase: ultra-slow contraction with w >>1 Erickson, Wesley, PJS. Turok Erickson, Gratton, PJS, Turok H = 2 0 8G m 3 a 3 0 8G r 3 a 4 0 2 a 6 8G 3 a 3 (1w ) ... k a2 inflaton w >> 1 N.B. Do not need finely tuned initial conditions or inflation or dark energy … ekpyrotic phase: ultra-slow contraction with w >>1 Erickson, Wesley, PJS. Turok Erickson, Gratton, PJS, Turok H = 2 0 8G m 3 a 3 0 8G r 3 a 4 0 2 a 6 8G 3 a 3 (1w ) ... k a2 inflaton w >> 1 … and avoid chaotic mixmaster behavior … ekpyrotic phase: ultra-slow contraction with w >>1 Erickson, Wesley, PJS. Turok Erickson, Gratton, PJS, Turok H = 2 0 8G m 3 a 3 0 8G r 3 a 4 0 2 a 6 8G 3 a 3 (1w ) ... k a2 inflaton w >> 1 … and Hsmoothing << Hnormal and contracting ekpyrotic phase: ultra-slow contraction with w >>1 Erickson, Wesley, PJS. Turok Erickson, Gratton, PJS, Turok H = 2 0 8G m 3 a 3 0 8G r 3 a 4 0 2 a 6 8G 3 a 3 (1w ) ... k a2 inflaton w >> 1 … and scale-invariant perturbations of scalar fields. How to get w >> 1 ? V “branes” Field-theory 2 V ( ) w = 2 1 V ( ) 1 2 1 2 Curiously, precision tests can distinguish the two key qualitative differences between inflation and ekpyrotic/cyclic models • Hsmoothing is exponentially different gravitational waves • w is orders of magnitude different local non-gaussianity “local” non-gaussianity generated when modes are outside the horizon (“local” NG) z=zL+ 2 f z L 5 NL 3 Maldacena Komatsu & Spergel “intrinsic” NG contribution (positive fNL) 3 depending on e = (1 + w) 2 or steepness of potential int f NL ~ e ek e conv ~ wek wconv