* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download On the Shoulders of Giants”
Bra–ket notation wikipedia , lookup
Relational approach to quantum physics wikipedia , lookup
Laplace–Runge–Lenz vector wikipedia , lookup
Centripetal force wikipedia , lookup
Perturbation theory (quantum mechanics) wikipedia , lookup
Derivations of the Lorentz transformations wikipedia , lookup
Renormalization group wikipedia , lookup
Four-vector wikipedia , lookup
Double-slit experiment wikipedia , lookup
Introduction to quantum mechanics wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Quantum logic wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Nuclear structure wikipedia , lookup
Joseph-Louis Lagrange wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Statistical mechanics wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Classical central-force problem wikipedia , lookup
Photon polarization wikipedia , lookup
Uncertainty principle wikipedia , lookup
Work (physics) wikipedia , lookup
Matter wave wikipedia , lookup
Matrix mechanics wikipedia , lookup
Old quantum theory wikipedia , lookup
Quantum chaos wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Canonical quantization wikipedia , lookup
Equations of motion wikipedia , lookup
Path integral formulation wikipedia , lookup
Noether's theorem wikipedia , lookup
Classical mechanics wikipedia , lookup
First class constraint wikipedia , lookup
Lagrangian mechanics wikipedia , lookup
Dirac bracket wikipedia , lookup
Routhian mechanics wikipedia , lookup
QM 480
“On the Shoulders of Giants”
An Introduction to Classical
Mechanics
QM 480
If I have seen further it is by standing on
the shoulders of giants.
Isaac Newton, Letter to Robert Hooke,
February 5, 1675
English mathematician & physicist (1642 1727)
QM 480
Quantum Mechanics (QM) is based on classical
mechanics. It combines classical mechanics
with statistics and statistical mechanics.
For native English-speakers, it is somewhat
unfortunate that it uses the word “quantum”. A
better English word which describes the thrust
of this approach would be “pixel”.
QM 480
2nd Century BC
Lights! Camera! Action!
Hero of Alexandria found that light, traveling from one point to
another by a reflection from a plane mirror, always takes the
shortest possible path.
1657
Pierre de Fermat reformulates the principle by postulating that
the light travels in a path that takes the least time!
In hindsight, if c is constant then Hero and Fermat are in
complete agreement.
Based on his reasoning, he is able to deduce both the law of
reflection and Snell’s law (nsinQ = n’ sinQ’)
QM 480
An Aside
Fermat is most famous for his last
theorem:
Xn +Yn = Zn where n=2 and …
On his deathbed, he wrote:
And n= arrgh! I’m having a heartattack!
His last theorem was only solved by
computer in the last 10 years…
QM 480
1686
Now we wait for the Math
The calculus of variations is begun by Isaac
Newton
1696
Johann and Jakob Bernoulli extend
Newton’s ideas
QM 480
1747
Pierre-Louise-Moreau de Maupertuis asserts a
“Principle of Least Action”
More Theological than Scientific
“Action is minimized through the Wisdom of God”
His idea of action is also kind of vague
Now we can get back
Action (today’s definition)—
Has dimensions of length x momentum or energy x
time
Hmm… p * x or E*t … seems familiar…
QM 480
To the Physics
1760
Joseph Lagrange reformulates the principle
of least action
The Lagrangian, L, is defined as L=T-V
where T= kinetic energy of a system and
V=potential energy of a system
QM 480
Hamilton’s Principle
1834-1835
William Rowan Hamilton’s publishes two
papers on which it is possible to base all of
mechanics and most of classical physics.
Hamilton’s Principle is that a particle follows
a path that minimizes L over a specific time
interval (and consistent with any constraints).
A constraint, for example, may be that the
particle is moving along a surface.
QM 480
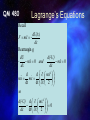
Lagrange’s Equations
Recall
dU(x)
F mx dx
Rearrangin g
dU
d(-U)
mx 0 and
mx 0
dx
dx
d
d mx 2
mx mx
dt
dt x 2
so
d(-U) d mx 2
0
dx
dt x 2
QM 480
Lagrange’s Equations
Now
mx 2
0 and
x 2
U ( x) 0
x
And I can add zero to anything and not change the result
d mx 2
d mx 2
-U ( x)
U ( x) 0
dx 2
dt x 2
but
mx 2
T
2
Thus
and
dL d L
0
dx dt x
L T V
QM 480
Expanding to 3 Dimensions
Since x, y, and z are orthogonal and linearly
independent, I can write a Lagrange’s EOM for each.
In order to conserve space, I call x, y, and z to be
dimensions 1, 2, and 3.
So
dL d L
0 i 1,2,3
dqi dt qi
Amusingly enough, 1, 2, 3, could represent r, q, f
(spherical coordinates) or r, q, z (cylindrical) or any
other 3-dimensional coordinate system.
QM 480
Example: Simple Harmonic
Oscillator
Recall for
SHO: V(x)=
½ kx2 and let
T=1/2 mv2
Hooke’s Law:
F=-kx
dL d L
0
dq dt q
1 2 1 2
L mx kx
2
2
dL d 1 2
kx kx
dx dx 2
L 1 2
d
mx mx and mx mx
x x 2
dt
so
kx mx 0 or kx mx
QM 480
Tip
The trick in the Lagrangian Formalism
of mechanics is not the math but the
proper choice of coordinate system.
The strength of this approach is that
1.
Energy is a scalar and so is the Lagrangian
2.
The Lagrangian is invariant with respect to
coordinate transformations
Two
Conditions
Required
for
QM 480
Lagrange’s Equations
1.
The forces acting on the system (apart
from the forces of constraint) must be
derivable from a potential i.e. F=-dU/dx
or some similar type of function
2.
The equations of constraint must be
relations that connect the coordinates of
the particles and may be functions of
time.
QM 480
Your Turn
Projectile:
Go to the board and work a simple projectile
problem in cartesian coordinates. Don’t worry
about initial conditions yet.
Now do the same in polar coordinates.
Hint:
2
1 2 1
mr m rq
2
2
U mgr sin q
T
QM 480
Introducing the Hamiltonian
First, any
Lagrangian which
describes a uniform
force field is
independent of time
i.e. dL/dt=0.
L L(q, q )
dL L q L q L
dt q t q t t
dL L
L
q
q
dt q
q
L d L
Since
q dt q
dL
d L L
q
q
dt
dt q q
QM 480
Introducing the Hamiltonian
dL
d L L
d L
q
q q
dt
dt q q
dt q
d L dL d L
0 q
q
L
dt q dt dt q
So
L
q
L a constant H
q
Hmmm… H for Hornblower or Hamilton?
QM 480
Introducing the Hamiltonian
L
L H
q
L T (q ) V (q ) T
q
q
q
1
T
T
If T mq 2
mq q
mq 2 2T
2
q
q
So
q
2T (T V ) T V H
but
T V E (mechanical energy!)
QM 480
H is only E when
It is important to note that H is equal to E only if
the following conditions are met:
The kinetic energy must be a homogeneous
quadratic function of velocity
The potential energy must be velocity independent
While it is important to note that there is an
association of H with E, it is equally important
to note that these two are not necessarily the
same value or even the same type of quantity!
Making
Simple
Problems
QM 480
Difficult with the Hamiltonian
Most students find that the Lagrangian
formalism is much easier than the
Hamiltonian formalism
So why bother?
Making
Simple
Problems
QM 480
Difficult with the Hamiltonian
First, we need to define one more quantity:
generalized momenta, pj
L
pj
where j 1,2,3
q j
So H q
L
L becomes
q
3
H pq L or H p j q j L
j 1
QM 480
SHO with the Hamiltonian
1 2 1 2
L mx kx
2
2
L
p
p2
p
mx x 2 x 2
q
m
m
So H pq L becomes
p
p2 p2 1 2
H p L
kx
m
m 2m 2
p2 1 2
H
kx
2m 2
Big deal, right?
But look what we did
L=f(q,dq/dt,t)
H=f(q,p,t)
So our mechanics all
depend on momentum
but not velocity
Recall light has constant
velocity, c, but a
momentum which is
p=hc/l !
QM 480
The Big Deal
So if we are going to define mechanics
for light, it does not make any sense to
use the Lagrangian formulation, only the
Hamiltonian!
QM 480
That Feynman Guy!
Richard Feynman thought that Lagrangian
mechanics was too powerful a tool to ignore.
Feynman developed the path integral
formalism of quantum mechanics which is
equivalent to the picture of Schroedinger and
Dirac.
So which is better? Both and Neither
There seems to be no undergraduate treatment of
path integral formalism.
QM 480
Hamilton’s Equations of
Motion
Just like Lagrangian formalism, the Hamiltonian
formalism has equations of motion. There are
two equations for every degree of freedom
They are
H
q
p
H
p
q
QM 480
p2 1 2
H
kx
2m 2
H p
x
p m
H
p
kx or
q
dp
Since F
p
dt
F kx
Finishing the SHO
p kx
Hooke’s Law again!
QM 480
H
q
p
H
p
q
Symmetry
Note that Hamilton’s EOM
are symmetric in
appearance i.e. that q and
p can almost be
interchanged!
Because of this symmetry,
q and p are said to be
conjugate
QM 480
Definition of Cyclic
Consider a Hamiltonian of a free particle i.e.
H=f(p)… then – dp/dt=0 i.e. momentum is a
“constant of the motion”
Now in the projectile problem, U=-mgy and for
x-component, H=f(px) only!
Thus, px= constant and the horizontal variable, x is
said to “cyclic”!
A more practical definition of cyclic is “ignorable” and
modern texts sometimes use this term.
QM 480
Definition of canonical
Canonical is used to describe a simple, general
set of something … such as equations or
variables.
It was first introduced by Jacobi and rapidly
gained common usuage but the reason for its
introduction remained obscured even to
contemporaries
Lord Kelvin was quoted as saying “Why it has
been so called would be hard to say”
QM 480
Poisson Brackets
Poisson Bracket of u and v with respect to the canonical variables q and p
is defined as
u v v u
{u , v}
q p q p
What if u and v were functions of q and p?
{qi , q j } 0
Example {x, y}
x y y x
0
x p x y p y
{ pi , p j } 0
{qi , p j } i , j { pi , q j }
QM 480
Kronecker Delta
i,k=1
if i=k
i,k=0
if i≠k
QM 480
Back to Fish
Consider two continuous functions g(q,p) and
h(q,p)
If {g,h}=0 then h and g are said to commute In other
words, the order of operations does not matter
If {g,h}=1 then quantities are canonically conjugate
• A look ahead: we will find that canonically conjugate
quantities obey the Uncertainty principle
QM 480
Properties of Fish
The following are properties of the Poisson Bracket
dg
g
a)
{g , H }
dt
t
where H Hamiltonia n H H(q, p)
b) q j {q j , H }
c)
p j { p j , H }
QM 480
Levi-Civita Notation
Consider t he vector product of A and B
C AB
The individual components can be expressed in a compact
notation
Ci ijk A j Bk
j ,k
where
ijk
if any index equals any other
0
1 if i, j, k is an even permuation of 1, 2,3
- 1 if i, j, k is an odd permutatio n (out of order)
122 112 133 0
123 312 231 1
213 321 132 1
QM 480
Levi-Civita Notation
Consider t he vector product of A and B
1̂ 2̂
C A1 A2
B1 B2
Consider
3̂
A3
B3
C1 A2 B3 A3 B2
123 1
132 1
C1 123 A2 B3 132 A3 B2