Download BBA IInd SEMESTER EXAMINATION 2008-09

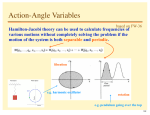
B.Sc. (Hons) Physics III (Third) Semester Examination
2013-14
Course Code: BAS306
Paper ID: 0983208
Classical Physics
Time: 3 Hours
Max. Marks: 70
Note: Attempt six questions in all. Q. No. 1 is compulsory.
1.
a)
b)
c)
d)
e)
f)
g)
h)
2. a)
b)
Answer any five of the following (limit your answer to 50
words).
(4x5=20)
What are generalized coordinates? Distinguish a system on
the basis of time dependence of generalized coordinates.
Show that for a single particle with constant mass, the
differential equation for kinetic energy is

dT
 F .v . where T is kinetic energy
dt
Using Hamilton’s principle show that the shortest distance
between two points is a straight line joining them.
Explain the condition for a transformation to be canonical.
Show that the transformations
Q  p and
P   q are canonical transformations.
Obtain Hamilton’s equations for a charged particle moving in
an electromagnetic field.
Show that the central force motion of two bodies about their
center for mass can be reduced to an equivalent one body
problem.
Using Poisson brackets, obtain Jacobi identity.
Derive Lagrange’s equations in presence of non conservative
forces.
(5)
Explaining the velocity dependent potential. Write the
expression for the velocity dependent potential of
electromagnetic field.
(5)
3.
Apply Hamilton’s principle to derive Lagrange’s equation.
Using Hamilton’s principle, find the equation of motion of
one dimensional harmonic oscillator.
(10)
4.
Discuss the advantages of using a Lagrangian for the
description of a system. Use Lagrangian to establish analogy
between an electrical and a mechanical system.
(10)
5.
What are non-holonomic systems? Apply the Lagrange’s
method of undetermined multipliers to the problem of a hoop
rolling down an inclined plane without slipping.
(10)
6.
What is the objective of Legendre transformation? Derive
Legendre transformation and apply it to generate a
thermodynamic quantity.
(10)
7.
Define canonical transformations and generating function.
Obtain the transformation equations corresponding to various
generating functions.
(10)
8.
Explain action angle variable. Obtain the solution of
harmonic oscillator problem by action angle variable.
(10)