Download Modern Physics - Politechnika Wrocławska

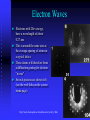
Modern Physics
Lecture IX
The Quantum Hypothesis

In this lecture we examine the evidence for
“light quanta” and the implications of their
existence



Waves as Particles
 The photoelectric effect
 Compton scattering
Particles as Waves
 Electron diffraction
The Double Slit Revisited
Photoelectric effect
When
light strikes the cathode, electrons
are emitted
Electrons moving between the two plates
constitute a current
Photoelectric Effect
Properties
of the photoelectric
effect
Electrons are only emitted above a
certain “cut-off” frequency

This frequency is different for different
materials


It is called the “work function”
Below the “work function” no electrons
are emitted no matter how intense the light
is

The maximum energy of the ejected
electron is Kmax=eDVs

Photoelectric Effect

Properties




No photoelectrons are emitted if the
frequency falls below some cut-off
frequency fc
The maximum energy of the photons is
independent of the light intensity
The maximum kinetic energy of the
photoelectrons increases with increasing
frequency
Photoelectrons are emitted almost
instantaneously from the surface
Photoelectric Effect

Explanation



Einstein extended Planck’s explanation for blackbody
radiation to suggest that in fact the quanta of energy used in
blackbody radiation are in fact localised “particle like”
energy packets
Each having an energy given by hf
Emitted electrons will have an energy given by
K max  hf  f

Where f is known as the “work function” of the material
Photoelectric Effect

Quantum interpretation




If the energy of a photon is less than the work function f, the
photon cannot give enough energy to the electron to leave the
surface
Kmax does not depend on light intensity, because doubling the
number of photons would only double the number of
electrons and not double their energy
Kmax increases with frequency because energy and frequency
are related
If light is particle-like, then all of the energy will be delivered
instantaneously thus liberating an electron with no time delay
between the light hitting the surface and the electron escaping
Inverse photoelectric effect - Production of X-rays
X-rayphoton s
E lectrons
High vol tage
1.
Photons are absorbed in whole - electrons can transfer part of
their energy.
2.
Brehmsstrahlung - electrons decelerate in electromagnetic field
of nuclei: Ef = Ei - h , wide distribution
3.
Maximal frequency - minimal wavelength (observed empirically
first) eV = h max = h c / min
4.
Also discrete spectrum (atomic levels)
Roentgen Lamp
me v 2
hc
 eVAC  hf max 
2
 min
Tungsten - wolfram
Compton Scattering



If light is like a particle does it have momentum?
In Compton scattering x-rays impart momentum to matter,
scattering electrons like billiard balls
Thus photons also have momentum. The momentum of a photon
is given by
E hf h
p 

c
c 
Recoiling electron
f

Incident
Photon, 0
   0 
Scattered
Photon, ’
h
(1  cos  )
me c
Photons and Electromagnetic
Waves


How can light be considered a photon (particle)
when we know it is a wave
Light has a dual nature: it exhibits both wave and
particle characteristics



There is a smooth transition of these properties across the
electromagnetic spectrum
At low frequencies (radio waves) photons have a vanishingly small
energy and the wave properties dominate
At high frequencies (x-rays, g-rays) it is the particle properties that
dominate
But…
Louis de Broglie
1892 - 1987
Wave Properties of Matter



In 1923 Louis de Broglie postulated that perhaps matter
exhibits the same “duality” that light exhibits
Perhaps all matter has both characteristics as well
Previously we saw that, for photons,
p
E hf h


c
c 

Which says that the wavelength of light is related to its
momentum

Making the same comparison for matter we find…

h
h

p mv
de Broglie Wavelength of Electrons
We now calculate the wavelength of a charged particle
accelerated through potential V
 Assume that the particles have mass m and charge q
 Equate kinetic energy of the particles with the electrostatic
energy
K = m v 2/2 = q V
momentum
p=mv
We can express kinetic energy in terms of momentum
K = p 2/(2 m) = q V
Reorganise to get
p = (2 m q V )1/2
de Broglie’s hypothesis gives
=h/p
h
λ
Substitute for p to get
1/2

2 m q V 
Does Matter Really Have a
Wavelength



The wavelength of matter waves is very small.
This is why we do not see them in our every day
experience
To see diffraction a grating a very small slit width
is required (eg the space between two atoms in a
crystal)
This is exactly how electron diffraction was first
found!

G. P. Thompson of Scotland and Davisson and Germer from the
USA used the close spacing between atoms in a crystal lattice to
diffract electron waves thus proving that matter can also exhibit
diffraction and interference
Sir Joseph John (JJ) Thomson
C.J.Davisson and L.G.Germer
diffraction
dNi=0.215nm
  d sin   0.165nm
de Broglie
eVba
p2

2m
h
h
 
 0.167 nm
p
2meVba
scattered through angle . Note that 2 f +  =
180°, i.e. f  90°- /2
• The condition for constructive interference is
2 d sinf = n 
n integer
Figs. from R. Eisberg & R. Resnick Quantum Physics
Example of Measuring the Lattice
Spacing
 Consider an electron accelerated to V = 50 V
Example




Electron scattering in nickel
Electrons are accelerated through V = 54V.
The maximum of scattering is found to be at f = 65 °
( = 50 °)
Calculate the lattice spacing for nickel
h

1/2
2 m qV 
2 d = n  / sinf
Verify that d = 0.092 nm
Figs. from R. Eisberg & R. Resnick Quantum Physics

Electron interference
a, b, c – computer simulation
d - experiment
Electron Microscope
Electron Waves




Electrons with 20ev energy,
have a wavelength of about
0.27 nm
This is around the same size as
the average spacing of atoms in
a crystal lattice
These atoms will therefore form
a diffraction grating for electron
“waves”
Several pictures are shown left
(see the web links on the course
home page)
http://www.chem.qmw.ac.uk/surfaces/scc/scat6_2.htm
from this lecture…


The solution to the blackbody spectrum leads to the concept of photons, and to
a solution for the photoelectric effect
The maximum excess energy of a photoelectron is
K max  hf  f

The particle nature of light is also shown by Compton scattering of electrons
by photons
   0 

Scattering shows that photons have momentum given by
p

E hf h


c
c 
This implies that matter also has wavelike properties given by the de Broglie
formula


h
(1  cos  )
me c
h
h

p mv
The de Broglie wavelength leads to phenomena such as electron diffraction. A
common tool in modern crystallography