* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Meson spectroscopy - KVI - Center for Advanced Radiation
Quantum machine learning wikipedia , lookup
Double-slit experiment wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Atomic theory wikipedia , lookup
Scalar field theory wikipedia , lookup
Quantum key distribution wikipedia , lookup
Quantum group wikipedia , lookup
Renormalization group wikipedia , lookup
Copenhagen interpretation wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
EPR paradox wikipedia , lookup
Particle in a box wikipedia , lookup
Quantum state wikipedia , lookup
Matter wave wikipedia , lookup
Hidden variable theory wikipedia , lookup
Canonical quantization wikipedia , lookup
Nuclear force wikipedia , lookup
History of quantum field theory wikipedia , lookup
Wave–particle duality wikipedia , lookup
Hydrogen atom wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Elementary particle wikipedia , lookup
Light-front quantization applications wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
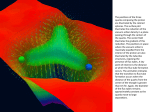
Meson spectroscopy Hybrid mesons and Multiquark states Samuel Hoekman Zorione Herrasti 1 Introduction • To understand the dynamics on quark scale one relies on lattice QCD and phenomological methods • Last time glueball spectroscopy was discussed as a way to confirm QCD by searching for exotic JPC quantum numbers • Another way is using hybrid mesons, since hybrid mesons are richer in number (theoretically…) • One can also search for exotic flavors: multi quarks 2 Overview • Hybrid meson (Zorione) • QCD (Zorione) • Flux Tube model (Zorione) – 3P0 pair creation • Phenomenological methods (Samuel) – Simulation • Monte Carlo Methods • Partial Wave Analysis • • • • • Conclusions (Samuel) Multi quarks (Samuel) MIT-bag model (Samuel) BES-II experiment (Zorione) Conclusions (Zorione) 3 Mesons • Formed by a quark antiquark pair. • Quantum numbers. - Parity (-1)l+1 - Charge conjugation (-1)l+s 4 Hybrid mesons • Quantum numbers for hybrid mesons - Quantum numbers that cannot be explained by the quark model. (JPC) - Formed by a q q pair plus one explicit gluon. - If kinematics and other conservation laws allow, the production cross section for hybrids, is expected to be the same as that for ordinary mesons. - Hybrid mesons and ordinary mesons with the same quantum numbers can mix freely. - Identification of hybrid mesons difficult unless they have exotic quantum numbers. 5 Quantum chromodynamics (QCD) • Seems to be the correct theory of the strong interactions. • The spectrum of QCD is probably richer than that of the naive quark model. • If we remove the quarks from QCD, there should remain a nontrivial color SU(3) which must have its own spectrum of states. • Constituent quark, constituent gluon.(q q g) • Gluonic degrees of freedom condensed into collective string like flux tube. 6 A QCD FLUX TUBE BETWEEN TWO QUARKS (sapac) A quark-antiquark pair, linked by a strong color field. The arrows point the direction of the color field. This system can have excitations with a vibration perpendicular to the axis. 7 Theoretical foundation of the flux tube model • In the Hamiltonian formulation of QCD on a cubic spatial lattice, – Quark degrees of freedom “live” on the lattice sites – Gluonic degrees of freedom “live” on the links between this sites. HQCDlattice = Hglue + Hquark • We define QCD field operators (Ul), on this lattice, the points are linked with Gauge transformations. • We can define: pure gluon states, or quark gluon states. a 8 The pure glue sector, the simplest states are “glue loops”. Energy: (2g2 /3a2)L g= coupling constant a=lattice spacing L=Length of the path The simplest quark containing state consits of a quark antiquark on the lattice joined by a path of flux links. Energy: mq+ mq +(2g2/3a2)L 9 The Flux tube model •The quarks move adiabatically in an effective potential generated by the dynamics of the flux tube. •The flux tube can rotate along its axis, but the orbital angular momentum along the flux tube is 0. •The ground state, well approximated by a pair q q with a string in its quantum-mechanical ground state. (Quark model, low frequency limit) • Hybrid mesons: Excitations of the color flux tube. 10 11 Hybrid mesons • There are two transverse polarization states of the string, clockwise (+) or anticlockwise (-) about the quark-antiquark axis. • We define an angular component momentum about the axis (Λ) – The dependence of the string wave function on the angle γ about the axis is eiγΛ • Λ= Σ (n m+ - n m- ) , nm+- mode occupation numbers • η p= (-1)L+Λ+1 • ηC= (-1)L+S+ΛΠm[(-1)m]n(m-) + n(m+) 12 - Lowest hybrids with one m=1 phonon, leading to among other possibilities, the exotic quantum numbers: JPC= 0+-, 1-+, 2+The complete set of quantum numbers to one phonon m=1: S=1, JPC= 2+-, 2-+, 1+-, 1-+, 0+-, 0-+ S=0, JPC= 1++, 1-Prediction of mass for different flavor hybrid mesons Flavor Mass (GeV) u,d 1.7- 1.8 s 1.9 c 4.2 b 10.8 13 EXAMPLE (1-+) L=1, S=1 J= 0, 1, 2 Λ= Σ (n m+ - n m- ) , η p= (-1)L+Λ+1 n(m+) ηC= (-1)L+S+ΛΠm[(-1)m]n(m-) + J=1 m=1 mode, nm+ =1, Λ=1 P= (-1)1+1+1= -1 C= (-1)1+1+1 (-1) = +1 14 3P 0 quark pair creation • The hybrid meson (A) can decay into two B, C mesons. • In the breaking process there´s no introduction of extra angular momentum • The relative angular momentum during the breaking process has (S=1, L=1, J=0). A B+C A B + C 15 • The angular momentum Λ, has to be absorbed. • Cannot decay into a pair of ground state mesons, as ππ, πη, πρ... • The preferential decay modes, those with one excited meson: b1π, f1π... 16 Isgur and Paton ’85 • Many decay channels are predicted from the FTM! 17 “Practical” part of hybrids • Easiest to search for lower lying states • For instance states with JPC=1-+ • Crystal Barrel Collaboration experiment ‘98 • Resonant behavior of P-wave @ 1.4 GeV • Experiment is ongoing @ BES-III • BESIII/GEANT4 sensitivity simulation • Monte Carlo simulation of J/ 0 18 Reaction: J/ 0 Energy diagram for the reaction: Kinematics of the reaction: 19 Simulation • Monte Carlo method • Define input domain, i.e. the decay channels • Generate the inputs using a prob. density • Compute a result • Generated input • • • • • 1(1400) ~ 14.57% a0(980) ~ 4.38% a1(1320) ~ 21.39% a2(1700) ~ 41.64% Background 20 Criteria for 1-+ candidates • Require two ‘good’ tracks with zero net charge (i.e. being a -+-pair for sure)… • Within polar angle region • 5 cm within interaction region • …and at least four ‘good’ photons • Energy deposit > 50 MeV in the EM calorimeter • Angles correspond to kinematics 21 Selection from data • Kinematic fit with criteria used as input Allow values to vary within uncertainty • Points with 2 < 15 were chosen • Constraint on the photons from 0 and decay: (M M 1 2 ) 2 (M M 3 4 ) 2 0 22 Results • Use invariant mass for products: M 2 ( Ei )2 ( pi )2 • The MCS shows three “resonances” 23 Partial Wave Analysis • Today: simplified PWA of elastic scattering in terms of plane waves interacting with a centre and spins 0 • Plane waves in spherical harmonics 24 Partial wave analysis • A result is the formula for the DCS: i d 1 e 1 2 | f ( ) | | (2l 1) Pl (cos ) |2 l d k l 0 2i • How about the resonances? Take the partial wave amplitude and let’s see: ei l 1 1 /2 2i cot l i ( ER E ) i / 2 d cot l ( E ) cot l ( E ) cot[ l ( ER )] ( ER E ) H .O. dE 0 ( ER E)2 / 25 Breit-Wigner fit • What follows is the Breit-Wigner formula for the cross section (here most general form): 4 2J 1 2 / 4 (J ) 2 2 2 k (2s1 1)( 2s2 1) ( ER E ) / 4 26 Results • Four fits appear for the different resonances: a2* a2 a0 1 27 Results • The simulation was good, the angular distributions shows no irregularities 28 Conclusions • The results from PWA correspond to the input values from MC • So with the setup at BES-III these resonances can be identified (if they exist) 29 Multi quarks: confinement • A multiquark state is formed if there are more than four quarks confined in a so called MIT-bag • The Dirac eqn. gives with appropriate boundary conditions a zero normal quark flow • To conserve energy and momentum at the boundary, the external pressure is balanced by internal pressure 30 Multiquarks: measurement • Above a threshold value, the multiquark decays into mesons & baryons • So, such a state has a broad width (makes experiments difficult) • However, a number of new structures were seen in J/ decays 31 BES II Experiment • An anomalous enhancement near the mass threshold in the pp invariant mass-spectrum J/ψ γ pp • Theoretical interpretation of the pp mass threshold enhancement: pp bound state= baryonium • Baryonium interpretation of the pp mass enhancement requires a new resonance with a mass around 1.85 Gev/c2 32 Observation of X(1835) in J/Ψ J/ψ γπ+π-η’ γ Χ(1835) π+π- pp η’ π+ γ ρ ππ+π-η π+π- γγ 33 π0 π0 η η ω η’ η’ 34 Selection of candidates • • • • • Reject events Mγγ < 0.22 GeV/c2 and 0.72 GeV/c2< Mγγ < 0.82 GeV/c2 [Mγγ – mη] < 0.05 GeV/c2 [Mπ+π-η – mη´] < 0.015 GeV/c2 [Mπ+π- - mρ] < 0.2 GeV/c2 [Mγπ+π- - mη´] < 0.025 Gev/c2 Conclusion • To ensure that the peak near 1835 MeV/c2 is not due to background, extensive studies of potential background processes, using both data and MC have been made. • The main background channel J/ψ π0π-π+η´, and other background processes with multiphotons and /or kaons are reconstructed with data. • None of these background processes produce a peak around 1835 MeV/c2 in the π-π+η´ invariant-mass spectrum. Baryonium is a candidate for a 6 quark system. Summary • There is a wide field within QCD theory describing exotic mesons • Good tools to analyse meson spectroscopy are on the market • Measured decay channels at BES-III can be identified pretty well • There may be a 6 quark state which is a multi quark 37 Bibliography • IHEP-Physics-Report-BES-III-2008-001v1(chapters 9.4-9.5) • N.Isgur, R.Kokoski and J.Paton, Phys. Rev.Lett 54 (1985) 869 • N.Isgur and J.Paton, Phys.Rev. D31 (1985) 2910 • BES collaboration, M.Ablikim et al., Phys.Rev.Lett.95, 262001 (2005) • R. Jaffe, Phys. Rev. D17 (’78) 1444 • Any readable QM book • B. Muller, Gluon Quark Physics, Ch. 2