Download No Slide Title

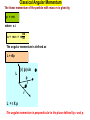
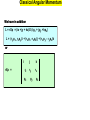
Classical Angular Momentum
Angular momentum in classical physics
Consider a particle at the position r
r
v
k
i
j
Where
r = ix + jy + kz
The velovcity of this particle is given by
dr
dx
dy
dz
v = dt = i dt + j dt + k dt
Classical Angular Momentum
The linear momentum of the particle with mass m is given by
p = mv
where e.i.
dx
px = mvx = m dt
The angular momentum is defined as
L = rXp
L
|r| |p| sin

p

r
L =rXp
The angular momentum is perpendicular to the plane defined by r and p.
Classical Angular Momentum
We have in addition
L = rXp = (ix + jy + kz)X ( ipx + jpy +kpz )
L = (r ypz - rz py)i + (r z px -r xpz )j + (r xpy - rypx)k
or
i
rXp =
rx
px
j
k
ry
rz
py
pz
Why are we interested in the angular
momentum ?
Consider the change of L with time
dL
dr
dp
=
Xp
+
rX
dt
dt
dt
dL
dp
=
mvXv
+
rX
dt
dt
Classical Angular Momentum
dp
= rX dt
dL
d
dr
d2 r
dt = rX dt [mdt ] = mrX dt2
dL
dt = mrXF
F = force
F
r
For centro-symmetric systems in which the force works in the same
direction as r we must have
dL
dt
= 0 : THE ANGULAR MOMENTUM IS CONSERVED
Classical Angular Momentum
Examples :
movement of electron around nuclei
movement of planets around sun
For such systems L is a constant of motion, e.g. does not change with
time since
dL
dt = 0
In quantum mechanics an operator O representing a constant of motion
will commute with the Hamiltonian which means that we can find
eigenfunctions that are both eigenfunctions to H and O