Download Chapter 7

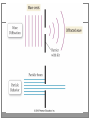
Quantum Mechanical Model
CHM 108
SUROVIEC
FALL 2015
I. Quantum Mechanics
2
 Small is a relative term, but we use it to show size.
 There is a limit to how we can use it in science.
II. Nature of Light
3
A. Wave Nature of light
Light is electromagnetic radiation. A type of energy
embodies in oscillating electric and magnetic fields
A. Wave Nature of Light
4
 An EM wave can be characterized by its amplitude
and wavelength.
A. Nature of Light
5
 All waves are also characterized by frequency (n)
B. The EM Spectrum
6
 The EM Spectrum is made of several different
wavelengths
C. Interference and Diffraction
7
 Waves (including EM waves) interact with each
other in a characteristic way called interference
07_06.JPG
8
D. Particle Nature of Light
9
 In the early 1900s light was believed to be wave only,
but then the photoelectric effect was discovered.
Example
10
 A DVD player uses a laser that emits light at 685nm.
What is the energy of 1 mole of photons of this light?
III. Atomic Spectroscopy and the Bohr Model
11
 The dual nature of light led scientists to think about
how light acts as both a particle and as a wave.
 Atomic Spectroscopy was developed to explore the
phenomenon.
07_10.JPG
12
III. Atomic Spectroscopy and the Bohr Model
13
 The idea that each element has discreet lines
required scientists, like Neils Bohr, to develop a new
model for the atom.
IV. Wave Nature
14
 It has been shown that the wave nature of an
electron is an inherent property of an individual
electron.
A. deBroglie Wavelength
 An electron traveling through space has a wave
nature.
Example
15
 Calculate the wavelength in nm of an electron with
speed 4.57 x 106 m/s
B. Uncertainty Principle
16
 Experiments have shown that we can never see the
interference pattern and simultaneously determine
which hole the electron goes through to make it.
C. Indeterminacy
17
 Macroscopic objects have their velocity and position
known : determined.
 Electrons do not (Uncertainty Principle):
indeterminacy
V. Quantum Mechanics and the Atom
18
 Many properties of an element is dependent on the
energy of electrons which is related to the velocity
which we have shown to be indeterminate.
A.Schrodinger Equation
 The wave function ψ is away to describe energy of
electrons and the probability of finding an electron
in a volume of space.
1. Principle Quantum Number (n)
19
 The integer that determines overall size and energy
of an orbital.
2. Angular Momentum Quantum Number (l)
20
 This number determines the shape of the orbital.
2. Angular Momentum Quantum Number (l)
21
3. Magnetic Quantum Number (ml)
22
 This number tells us the orientation of the orbital
ml = -1
ml = -2
ml = 0
ml = -1
ml = 0
ml = 1
ml = 1
ml = 2
4. Magnetic Spin Number (ms)
25
 The spin of the electron in the orbital
Examples
26
 How many 2p orbitals are there in an atom?
 How many electrons can be placed in the 3d
sublevel?