Download Climate Change Science and Engineering

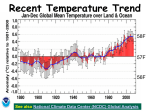
CE 401
Climate Change Science and Engineering
solar input, mean energy budget, orbital
variations, radiative forcing
20 January 2011
any questions from last time?
we got into solar inputs and Earth radiation budget
HW 2 is due today – will go over briefly on Tuesday
HW 3 is posted on the web - due Tuesday 1/25
HW 4 is posted on the web – due Thursday 1/27

energy radiated to space is = s 4p R2 Te4 [the Stefan-Boltzmann law]
where
s = Stefan-Boltzmann constant = 5.67 x 10-8 [w m-2 K-4]
342 w m-2 is the average energy input to the Earth system
242 w m-2 is the average radiated energy from the Earth
system, all radiated in the infrared part of the spectrum
radiative forcing: IPCC
“Radiative forcing is a measure of the influence a factor has in altering the balance of
incoming and outgoing energy in the Earth-atmosphere system and is an index of the
importance of the factor as a potential climate change mechanism. In this report
radiative forcing values are for changes relative to preindustrial conditions defined
at 1750 and are expressed in watts per square meter (W/m2)”
RF can be used to estimate a subsequent change in equilibrium temperature (DT) since
temperature must be related to change in radiation (linear or ??):
DT = l DF
where DF is the radiative forcing (W m-2), and
l is called the mean climate sensitivity factor [°C/(W m-2)] and allows computation of impacts
on temperature of different GHG
different atmospheric models  different values of l
RF for CO2,
l = 0.71 °C/W m-2 
for a 1°C atmospheric temperature change, DF = 1.41 W m-2
factors that influence the radiative equilibrium of the Earth system
average solar input: 342 w/m2
source IPCC 2007
global warming potential (GWP) of a gas GWPg:
a weighting factor to compare the GHG efficiency of a gas relative to CO2. Compares
potency of GHG to that of CO2:
GWPg =

Fg x Rg(t) dt /
F
CO2
x RCO2 dt
where the integral is from time 0 to time T
Fg = radiative forcing efficiency of the gas in question [w m-2 kg-1]
FCO2 = radiative forcing efficiency of CO2 [w m-2 kg-1]


Rg = fraction of the 1 kg of gas remaining in the atmosphere at time t
RCO2 = fraction of the 1 kg of CO2 remaining in the atmosphere at time t
radiative forcing efficiency is usually an exponential decay function, or ~ constant
with time, depending on the gas. For CO2 the decay is rapid the first few
decades as the biosphere absorbs the carbon, then it decays at a much
slower rate corresponding to the slow CO2 uptake of the oceans
Choice of time horizon for GWP depends on what a policy maker is interested in
e.g. CH4 GWP is 62 for 20 yr horizon, 23 for 100 yr, and 7 for 500 yr
compare CO2 to CH4 and N2O emissions for warming potential:
emissions:
CO2 = 27,000 MMt CO2/yr US emissions
CH4 = 370 MMtCH4/yr
N2O = 6 MMt N2O/yr
[MMt = million metric tons]
compare impacts to CO2:
CH4: GWP100 = 23*370 = 8510 MMtCO2 equivalent
N2O: GWP100 = 296*6 = 1776 MMtCO2 equivalent
details of greenhouse gases

radiation of the Earth at equilibrium effective temperature of 288K = +15°C
peak of the
radiation curve
at about 15 µm
this curve is the Planck curve
for a black body at 288K
CO2 as a molecular absorber
H2O as a molecular absorber
O3 as a molecular absorber
CH4 as a molecular absorber
blow up the CO2 graph to see what the absorbance looks like
blow up the CO2 graph to see what the absorbance looks like
rotational spectral lines of CO2
blow up the CO2 graph to see what the absorbance looks like
two spectral features
of CO2
molecular spectral “lines” are caused by quantized rotational energy transitions – changing
energy states due to different rotational states of the atoms  quantized spectra showing lines
at different energies (energy proportional 1/wavelength). In the IR, different sets of rotational
spectra are seen at different quantized levels of vibrational energy states of the molecule
diatomic molecule – two atoms rotating, vibrating, and
with electron energy transitions – all quantized
so if the energy levels are quantized (monochromatic), there shouldn’t the spectral lines be
monochromatic and thus have no spectal width in wavelength (energy) space?
Obviously the molecular lines DO have some energy width – why?
The ability of the molecule to absorb in the atmosphere depends on its quantum structure 
the intrinsic ability to absorb energy (light) and the abundance of the molecule in the
atmosphere.
The ability of an IR molecular absorber to be a greenhouse gas depends on the two parameters
above, and also how the spectrum lines up with the Earth IR radiation curve. Note that
there is a huge CO2 molecular band located nearly at the peak intensity of the Earth radiation
curve
the molecules absorb light (energy) from the Earth, change quantum state to a higher energy
level, and radiate that energy into all directions statistically. The radiation from the Earth
is moving skyward, after absorption and re-emission, it is moving in any direction  a net
drop in outward moving energy  the temperature of the radiating body must increase in order
to establish an equilibrium with incoming radiation from the sun.
• astronomical forces also drive global climate change
• seasons are driven by astronomical causes, as is the 24 h day/night cycle
Earth orbital changes that vary the solar input and cause the ice ages: the
Milankovich cycles – these cycles change the solar input to the Earth system
eccentricity changes
varies from nearly circular
to high eccentricity 0.058
with mean 0.028.
Caused by perturbations
from the other planets
e = 0.017 currently
shape of earth’s orbit changes during a cycle of about 100,000 years
axial tilt (obliquity) – increased obliquity  increased seasonal amplitude change
axis of rotation changes from about 21.5° to 24.5° --> seasonal variations over a period of
41,000 years. Tilt is the most significant cause of seasonal temp change. Modulates the
seasons, does not change climate overall
axial precession – trend in direction of axis of rotation in inertial space – gyroscopic motion
the earth’s rotation axis precesses (wobbles) with a period of about 26,000 years
due to tidal forces exerted by sun and moon on solid Earth since Earth is not spherical
affects climate extremes
problems with the Milankovitch theories:
• 100,000 yr problem: eccentricity variations should have a smaller impact that the other
mechanisms, but this is the strongest climate signal in the data record
• 400,000 yr problem: eccentricity variations also show a 400,000 yr cycle but that cycle is only
visible in climate records > 1My ago
• observations of climate changes show behavior much more intense than calculated
• the 23,000 yr cycle dominates, the opposite of what is observed
• so the explanation is not 100% - there are still issues with the explanation
deg change
obliquity=axial tilt
long of perihelion
precession index
calc. insolation to TOA
Benthic and Vostok
ice cores