Survey
* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download A Review of Basic Function Ideas
Document related concepts
History of the function concept wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Functional decomposition wikipedia , lookup
Positional notation wikipedia , lookup
Structure (mathematical logic) wikipedia , lookup
Dirac delta function wikipedia , lookup
Continuous function wikipedia , lookup
Bra–ket notation wikipedia , lookup
History of mathematical notation wikipedia , lookup
Interval arithmetic wikipedia , lookup
Elementary mathematics wikipedia , lookup
Musical notation wikipedia , lookup
Function (mathematics) wikipedia , lookup
Principia Mathematica wikipedia , lookup
Large numbers wikipedia , lookup
Multiple integral wikipedia , lookup
German tank problem wikipedia , lookup
Function of several real variables wikipedia , lookup
Abuse of notation wikipedia , lookup
Transcript
A Review of Basic
Function Ideas
Lesson 2.1
Definitions
Function: No x’s repeat (it is okay if the y’s
repeat). On a graph, you can use the
Vertical line test – each vertical line can
only touch one point on the line)
Domain: x’s
Range: y’s
Discrete set: countable set (days of week)
Non-discrete set: Numbers between 1 and
2
Example 1
The volume V of a sphere is a function
of its radius r. Suppose V = g(r)
a. Find a formula that defines g
g = 4/3 ∏ r3
b. use the formula to estimate the
volume of Earth, if it has a radius of
6380 km.
V = 4/3 * ∏ 63803
V = 1,088,000,000,000 km3
Interval Notation
Interval
Graph
Closed
a
Interval
Notation
Set
Notation
[a,b]
{x: a≤ x ≤ b}
(a,b)
{x: a < x < b}
[b, ∞)
{x: x≤ b}
(∞, a)
{x: x< a}
b
Open
a
b
Closed infinite
interval
b
Open infinite
interval
a
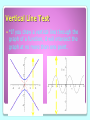
Vertical Line Test
*If you draw a vertical line through the
graph of a function, it will intersect the
graph at no more than one point.
Example 2
Use interval notation to describe the
domain of the real function t with rule
Bottom: (2x - 3)(2x Union
- 3) so x ≠ 3/2
Domain: (-∞, 3/2) U (3/2, ∞)
Example 3
Describe the set in interval notation:
The set of points on the number line that
are at least 3 units away from the point
-1.
(-∞, -4] U [2, ∞)
Homework
Page 84
2 – 20
(evens)
