Download and x > 1

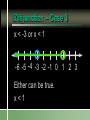
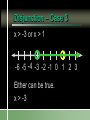
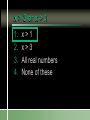
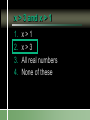
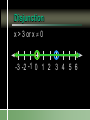
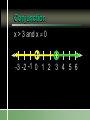
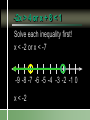
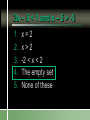
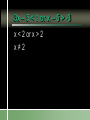
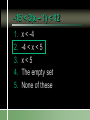
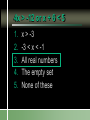
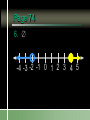
Compound Linear
Inequalities
Identify the Symbol
1.
2.
3.
4.
Less Than
Less Than or Equal To
Greater Than
Greater Than or Equal To
Identify the Symbol
1.
2.
3.
4.
Less Than
Less Than or Equal To
Greater Than
Greater Than or Equal To
Identify the Symbol
1.
2.
3.
4.
Less Than or Equal To
Greater Than or Equal To
All Real Numbers
Not Equal To
Identify the Symbol
1.
2.
3.
4.
Less Than or Equal To
Greater Than or Equal To
All Real Numbers
Not Equal To
Conjunction
 Mathematical sentences
joined by “and”
 Meaning: an intersection
Disjunction
 Mathematical sentences
joined by “or”
 Meaning: a union
Which is it?
 All students who have red
hair and are boys.
 All students who have
brown hair or wear glasses.
x < -3 and x > 1
Where on the number line are
both of these statements
true?
Solving Conjunctions
1. Graph both inequalities.
2. Find the intersection.
(overlapping portions)
3. Write the answer as an
inequality.
Conjunction – Case 1
x < -3 and x > 1
-6 -5 -4 -3 -2 -1 0 1 2 3
Conjunction – Case 1
 No overlap and arrows
going in the opposite
direction
 No solutions
Conjunction – Case 2
x > -3 and x < 1
-6 -5 -4 -3 -2 -1 0 1 2 3
Both must be true.
-3 < x < 1
Conjunction – Case 2
 Overlapping and arrows
going in the opposite
direction
 The solution is between the
two numbers.
Conjunction – Case 3
x < -3 and x < 1
-6 -5 -4 -3 -2 -1 0 1 2 3
Both must be true.
x < -3
Conjunction – Case 3
 Overlapping and arrows
going in the same direction.
 The solution will be a single
greater than/less than
inequality.
Conjunction – Case 3
x > -3 and x > 1
-6 -5 -4 -3 -2 -1 0 1 2 3
Both must be true.
x>1
Solving Disjunctions
1. Graph both inequalities.
2. Find the union. (Join the
two graphs)
3. Write the answer as an
inequality.
Disjunction – Case 1
x < -3 or x > 1
-6 -5 -4 -3 -2 -1 0 1 2 3
Disjunction – Case 1
 No overlap and arrows
going in the opposite
direction
 The solution is the original
inequalities.
Disjunction – Case 2
x > -3 or x < 1
-6 -5 -4 -3 -2 -1 0 1 2 3
Either can be true.
All Real Numbers
Disjunction – Case 2
 Overlapping and arrows
going in the opposite
direction
 If every part of the number
line is covered at least
once, then the solution is all
real numbers.
Disjunction – Case 3
x < -3 or x < 1
-6 -5 -4 -3 -2 -1 0 1 2 3
Either can be true.
x<1
Disjunction – Case 3
 Overlapping and arrows
going in the same direction.
 The solution will be a single
greater than/less than
inequality.
Disjunction – Case 3
x > -3 or x > 1
-6 -5 -4 -3 -2 -1 0 1 2 3
Either can be true.
x > -3
x > 3 or x > 1
1.
2.
3.
4.
x>1
x>3
All real numbers
None of these
x > 3 and x > 1
1.
2.
3.
4.
x>1
x>3
All real numbers
None of these
Disjunction
x > 3 or x  0
-3 -2 -1 0 1 2 3 4 5 6
Conjunction
x > 3 and x  0
-3 -2 -1 0 1 2 3 4 5 6
-2x > 4 or x + 8 < 1
Solve each inequality first!
x < -2 or x < -7
-9 -8 -7 -6 -5 -4 -3 -2 -1 0
x < -2
3x – 5 < 1 and x – 5 > -3
1.
2.
3.
4.
5.
x=2
x>2
-2 < x < 2
The empty set
None of these
3x – 5 < 1 or x – 5 > -3
x < 2 or x > 2
x≠2
-4 -3 -2 -1 0 1 2 3 4 5
-2 < x + 1 < 5
1. “x + 1 lies between -2 and
5.”
2. Always a conjunction.
3. Write as two separate
inequalities, then solve as
usual.
x + 1 > -2 and x + 1 < 5
-15 < 3(x – 1) < 12
1.
2.
3.
4.
5.
x < -4
-4 < x < 5
x<5
The empty set
None of these
4x > -12 or x + 6 < 5
1.
2.
3.
4.
5.
x > -3
-3 < x < -1
All real numbers
The empty set
None of these
Section 2.7
p. 74
Page 74
6. 
-4 -3 -2 -1 0 1 2 3 4 5
Page 74
8. 1 < x  7
10. All real numbers