* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download AC Circuits
Electric power transmission wikipedia , lookup
Superconducting magnet wikipedia , lookup
Wireless power transfer wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
National Electrical Code wikipedia , lookup
Residual-current device wikipedia , lookup
Hall effect wikipedia , lookup
Electric machine wikipedia , lookup
Faraday paradox wikipedia , lookup
Eddy current wikipedia , lookup
Electrical resistance and conductance wikipedia , lookup
Electricity wikipedia , lookup
Scanning SQUID microscope wikipedia , lookup
History of electrochemistry wikipedia , lookup
Earthing system wikipedia , lookup
Electrical substation wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Insulator (electricity) wikipedia , lookup
Power engineering wikipedia , lookup
Current source wikipedia , lookup
Three-phase electric power wikipedia , lookup
Stray voltage wikipedia , lookup
Induction heater wikipedia , lookup
History of electric power transmission wikipedia , lookup
Electromotive force wikipedia , lookup
Opto-isolator wikipedia , lookup
Mains electricity wikipedia , lookup
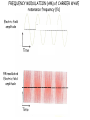
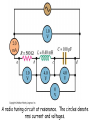
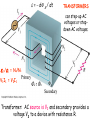
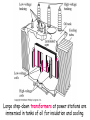
Alternating Current Ch. 31 Phasors and AC Resistance and reactance RLC series circuit Power in AC circuits Resonance in AC circuits Transformers C 2012 J. F. Becker (sec. 31.1) (sec. 31.2) (sec. 31.3) (sec. 31.4) (sec. 31.5) (sec. 31.6) Learning Goals - we will learn: ch 31 • How phasors make it easy to describe sinusoidally varying quantities. • How to analyze RLC series circuits driven by a sinusoidal emf. • What determines the amount of power flowing into or out of an AC circuit. • How an RLC circuit responds to emfs of different frequencies. Phasor diagram -- projection of rotating vector (phasor) onto the horizontal axis represents the instantaneous current. Notation: -lower case letters are time dependent and -upper case letters are constant. For example, i(t) is the time dependent current and I is current amplitude; VR is the voltage amplitude (= IR ). i(t) = I cos wt (source) vR(t) = i(t) R vR(t) = IR cos wt where VR = IR is the voltage amplitude. VR = IR Graphs (and phasors) of instantaneous voltage and current for a resistor. Graphs of instantaneous voltages for RLC series circuit. (The phasor diagram is much simpler.) i(t) = I cos wt (source) vL(t) = L di / dt vL(t) = L d(I cos wt )/dt vL(t) = -IwL sin wt E L I VL L I vL(t) = +IwL cos (wt + 900) where VL = IwL (= IXL) is the voltage amplitude and f = +900 is the PHASE ANGLE (angle between voltage across and current through the inductor). XL = wL Graphs (and phasors) of instantaneous voltage and current for an inductor. Graphs (and phasors) of instantaneous voltage and current showing phase relation between current (red) and voltage (blue). Remember: “ELI the ICE man” Crossover network in a speaker system. Capacitive reactance: XC =1/wC Inductive reactance: XL = wL Phasor diagrams for series RLC circuit (b) XL > XC and (c) XL < XC. Graphs of instantaneous voltages for RLC series circuit. (The phasor diagram is much simpler.) Graphs of instantaneous voltage, current, and power for an R, L, C, and an RLC circuit. Average power for an arbitrary AC circuit is 0.5 VI cos f = V rms I rms cos f. Instantaneous current and voltage: Average power depends on current and voltage amplitudes AND the phase angle f: The average power is half the product of I and the component of V in phase with it. The resonance frequency is at w = 1000 rad / sec (where the current is at its maximum) Graph of current amplitude I vs source frequency w for a series RLC circuit with various values of circuit resistance. AMPLITUDE MODULATION (AM) of CARRIER WAVE resonance frequency (fo) Electric field amplitude AM modulated Electric field amplitude FREQUENCY MODULATION (AM) of CARRIER WAVE resonance frequency (fo) Electric field amplitude FM modulated Electric field amplitude A radio tuning circuit at resonance. The circles denote rms current and voltages. e = - dF B / dt TRANSFORMERS can step-up AC voltages or stepdown AC voltages. e2 /e1 = N /N 2 V1I1 = V2I1 1 FB = FB Transformer: AC source is V1 and secondary provides a voltage V2 to a device with resistance R. (a) Primary P and secondary S windings in a transformer. (b) Eddy currents in the iron core shown in the crosssection AA. (c) Using a laminated core reduces the eddy currents. Figure 32.2b Large step-down transformers at power stations are immersed in tanks of oil for insulation and cooling. Figure 31.22 Figure 31.23 A full-wave diode rectifier circuit. (LAB) A mathematical model of Earth's magnetic field near the core. (Courtesy: Gary Glatzmaier) Review See www.physics.sjsu.edu/becker/physics51 C 2012 J. F. Becker PREPARATION FOR FINAL EXAM At a minimum the following should be reviewed: Gauss's Law - calculation of the magnitude of the electric field caused by continuous distributions of charge starting with Gauss's Law and completing all the steps including evaluation of the integrals. Ampere's Law - calculation of the magnitude of the magnetic field caused by electric currents using Ampere's Law (all steps including evaluation of the integrals). Faraday's Law and Lenz's Law - calculation of induced voltage and current, including the direction of the induced current. Calculation of integrals to obtain values of electric field, electric potential, and magnetic field caused by continuous distributions of electric charge and current configurations (includes the Law of Biot and Savart for magnetic fields). Maxwell's equations - Maxwell's contribution and significance. DC circuits - Ohm's Law, Kirchhoff's Rules, series-parallel combinations, power. Series RLC circuits - phasors, phase angle, current, power factor, average power. Vectors - as used throughout the entire course.