* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Document
Shape of the universe wikipedia , lookup
Riemannian connection on a surface wikipedia , lookup
Trigonometric functions wikipedia , lookup
Problem of Apollonius wikipedia , lookup
Algebraic geometry wikipedia , lookup
Analytic geometry wikipedia , lookup
Euler angles wikipedia , lookup
Lie sphere geometry wikipedia , lookup
Cartan connection wikipedia , lookup
Line (geometry) wikipedia , lookup
Geometrization conjecture wikipedia , lookup
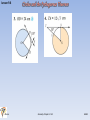
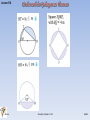
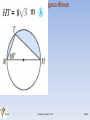
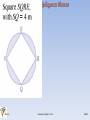
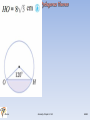
Lesson 9.6 In Chapter 6, you discovered a number of properties that involved right angles in and around circles. In this lesson you will use the conjectures you made, along with the , to solve some challenging problems. Let’s review two conjectures that involve right angles and circles. Tangent Conjecture: A tangent to a circle is perpendicular to the radius drawn to the point of tangency. Angles Inscribed in a Semicircle Conjecture: Angles inscribed in a semicircle are right angles. Tangent Segments Conjecture: Tangent segments to a circle from a point outside the circle are congruent. The following are two examples that use circle conjectures and dissections, special right triangles, and the JRLeon Geometry Chapter 9.6 HGSH Lesson 9.6 JRLeon Geometry Chapter 9.6 HGSH Lesson 9.6 JRLeon Geometry Chapter 9.6 HGSH Lesson 9.6 JRLeon Geometry Chapter 9.1-9.2 HGSH Lesson 9.6 JRLeon Geometry Chapter 9.1-9.2 HGSH Lesson 9.6 JRLeon Geometry Chapter 9.1-9.2 HGSH Lesson 9.6 JRLeon Geometry Chapter 9.1-9.2 HGSH Lesson 9.6 JRLeon Geometry Chapter 9.1-9.2 HGSH Lesson 9.6 Classwork: 9.6 Pages 509-510: problems 1 thru 16 JRLeon Geometry Chapter 9.1-9.2 HGSH