Geometry Module - Rice University Math
... calculator, The Geometer’s Sketchpad, and NonEuclid is incorporated into module materials. RUSMP’s Unique Qualifications to Write the Geometry Module RUSMP was established in 1987, with a grant from the National Science Foundation (NSF), in order to provide a bridge between the Rice University mathe ...
... calculator, The Geometer’s Sketchpad, and NonEuclid is incorporated into module materials. RUSMP’s Unique Qualifications to Write the Geometry Module RUSMP was established in 1987, with a grant from the National Science Foundation (NSF), in order to provide a bridge between the Rice University mathe ...
Geometry - Hickman County Schools
... midpoints, distances, and missing information in two and three dimensions. ...
... midpoints, distances, and missing information in two and three dimensions. ...
501 Geometry Questions
... the space they are in. To work with geometry you must understand the difference between representations on the page and the figures they symbolize. What you see is not always what is there. In space, lines define a square; on the page, four distinct black marks define a square. What is the difference? ...
... the space they are in. To work with geometry you must understand the difference between representations on the page and the figures they symbolize. What you see is not always what is there. In space, lines define a square; on the page, four distinct black marks define a square. What is the difference? ...
Document
... Determine whether each statement is true or false. If false, give a counterexample. 1. It two angles are complementary, then they are not congruent. 2. If two angles are congruent to the same angle, then they are congruent to each other. ...
... Determine whether each statement is true or false. If false, give a counterexample. 1. It two angles are complementary, then they are not congruent. 2. If two angles are congruent to the same angle, then they are congruent to each other. ...
Skills Practice Workbook - McGraw Hill Higher Education
... 11. If a figure is a triangle, then it has three sides. 12. If you find a penny, then you will have good luck. 13. If you ride your bicycle recklessly, then you can get hurt. 14. If two distinct lines intersect, then their intersection is one point. 15. If your cat purrs, then it is contented. ...
... 11. If a figure is a triangle, then it has three sides. 12. If you find a penny, then you will have good luck. 13. If you ride your bicycle recklessly, then you can get hurt. 14. If two distinct lines intersect, then their intersection is one point. 15. If your cat purrs, then it is contented. ...
Geometry EOI Practice 1. By the Law of Syllogism, what statement
... b. Apples make good pie. c. Delphie can make apple pie. d. Apple pie is made with sugar ...
... b. Apples make good pie. c. Delphie can make apple pie. d. Apple pie is made with sugar ...
Exploring Triangle Centers in Euclidean Geometry with the
... intersect in a point-unless the lines happen to be parallel, which is unusual. Thus concurrency is an expected property of two lines. But it is rare that three lines should have a point in common. One of the surprising and beautiful aspects of advanced Euclidean geometry is the fact that many triple ...
... intersect in a point-unless the lines happen to be parallel, which is unusual. Thus concurrency is an expected property of two lines. But it is rare that three lines should have a point in common. One of the surprising and beautiful aspects of advanced Euclidean geometry is the fact that many triple ...
Contemporary Arguments For A Geometry of Visual Experience
... This paper addresses an argument that has emerged in recent years from the work of James Van Cleve, Gideon Yaffe and Gordon Belot for a spherical geometry of visual experience. The argument in question consists of a demonstration that the geometry of what is visible and spherical geometry are equiv ...
... This paper addresses an argument that has emerged in recent years from the work of James Van Cleve, Gideon Yaffe and Gordon Belot for a spherical geometry of visual experience. The argument in question consists of a demonstration that the geometry of what is visible and spherical geometry are equiv ...
Proving that a Quadrilateral is a Parallelogram Any of the methods
... Name Honors Geometry Given: CirCle H and CirCle "Prove: HELO is a parallelogram ...
... Name Honors Geometry Given: CirCle H and CirCle "Prove: HELO is a parallelogram ...
Deductive geometry
... Learning about geometry includes being able to reason deductively and to prove logically that certain mathematical statements are true. It is important to be able to prove theories meticulously and step by step in order to show that the conclusions reached are soundly based. Mathematicians spend mos ...
... Learning about geometry includes being able to reason deductively and to prove logically that certain mathematical statements are true. It is important to be able to prove theories meticulously and step by step in order to show that the conclusions reached are soundly based. Mathematicians spend mos ...
Tangent circles in the hyperbolic disk - Rose
... Other geometries use some of these same axioms, but they may not use all of them. Axioms are statements that are universally accepted as true without requiring a proof. Hyperbolic geometry follows the first four of these axioms, but not the fifth axiom, the Parallel Postulate. One negation of the Pa ...
... Other geometries use some of these same axioms, but they may not use all of them. Axioms are statements that are universally accepted as true without requiring a proof. Hyperbolic geometry follows the first four of these axioms, but not the fifth axiom, the Parallel Postulate. One negation of the Pa ...
Geo 4.3to4.5 DMW
... congruent by showing that all six pairs of corresponding parts were congruent. The property of triangle rigidity gives you a shortcut for proving two triangles congruent. It states that if the side lengths of a triangle are given, the triangle can have only one shape. ...
... congruent by showing that all six pairs of corresponding parts were congruent. The property of triangle rigidity gives you a shortcut for proving two triangles congruent. It states that if the side lengths of a triangle are given, the triangle can have only one shape. ...
Geometry - Eleanor Roosevelt High School
... An indirect proof works because the negation of the statement to be proved is false, then we can conclude that the statement is true ...
... An indirect proof works because the negation of the statement to be proved is false, then we can conclude that the statement is true ...
congruent polygons
... Two polygons are congruent if and only if there is a correspondence between their sides and angles such that: 1. Each pair of corresponding angles is congruent. 2. Each pair of corresponding sides is congruent. homework Holt Geometry ...
... Two polygons are congruent if and only if there is a correspondence between their sides and angles such that: 1. Each pair of corresponding angles is congruent. 2. Each pair of corresponding sides is congruent. homework Holt Geometry ...
Worlds Beyond The Poles
... would have long since acquired land areas of the universe about us. There was no misinterpretation of signals by the seeker of 1926. He journeyed to the celestial beacons on the wings of extrasensory perception’s limitless necromancy. That magic permitted breaking through the long-established barrie ...
... would have long since acquired land areas of the universe about us. There was no misinterpretation of signals by the seeker of 1926. He journeyed to the celestial beacons on the wings of extrasensory perception’s limitless necromancy. That magic permitted breaking through the long-established barrie ...
geometry - Swampscott High School
... A diagram of part of a baseball field and some of its dimensions are shown below. Point F represents First Base, point S represents Second Base, point T represents Third Base, point H represents Home Plate, and point P represents another location on the baseball field. ...
... A diagram of part of a baseball field and some of its dimensions are shown below. Point F represents First Base, point S represents Second Base, point T represents Third Base, point H represents Home Plate, and point P represents another location on the baseball field. ...
Concurrent Lines, Medians, and Altitudes
... Because X has coordinates (1, 1) and Z has coordinates (5, 1), XZ lies on the horizontal line y = 1. The perpendicular bisector of XZ is the vertical line that passes through ( 1 + 5 , 1) or (3, 1), so the equation of the perpendicular ...
... Because X has coordinates (1, 1) and Z has coordinates (5, 1), XZ lies on the horizontal line y = 1. The perpendicular bisector of XZ is the vertical line that passes through ( 1 + 5 , 1) or (3, 1), so the equation of the perpendicular ...
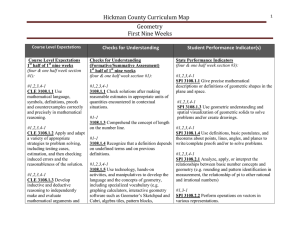
Mapping for Instruction - First Nine Weeks
... the formative assessment tests to be an effective instructional tool. Students will take a formative assessment test during the second, third, and fourth nine weeks which will contain materials from the previous nine weeks. Each teacher-designed test will assess current 9-weeks skill levels of the S ...
... the formative assessment tests to be an effective instructional tool. Students will take a formative assessment test during the second, third, and fourth nine weeks which will contain materials from the previous nine weeks. Each teacher-designed test will assess current 9-weeks skill levels of the S ...
6-3
... Both pairs of opposite sides have the same slope so and by definition, KLMN is a parallelogram. Holt McDougal Geometry ...
... Both pairs of opposite sides have the same slope so and by definition, KLMN is a parallelogram. Holt McDougal Geometry ...
Shape of the universe

The shape of the universe is the local and global geometry of the Universe, in terms of both curvature and topology (though, strictly speaking, the concept goes beyond both). The shape of the universe is related to general relativity which describes how spacetime is curved and bent by mass and energy.There is a distinction between the observable universe and the global universe. The observable universe consists of the part of the universe that can, in principle, be observed due to the finite speed of light and the age of the universe. The observable universe is understood as a sphere around the Earth extending 93 billion light years (8.8 *1026 meters) and would be similar at any observing point (assuming the universe is indeed isotropic, as it appears to be from our vantage point).According to the book Our Mathematical Universe, the shape of the global universe can be explained with three categories: Finite or infinite Flat (no curvature), open (negative curvature) or closed (positive curvature) Connectivity, how the universe is put together, i.e., simply connected space or multiply connected.There are certain logical connections among these properties. For example, a universe with positive curvature is necessarily finite. Although it is usually assumed in the literature that a flat or negatively curved universe is infinite, this need not be the case if the topology is not the trivial one.The exact shape is still a matter of debate in physical cosmology, but experimental data from various, independent sources (WMAP, BOOMERanG and Planck for example) confirm that the observable universe is flat with only a 0.4% margin of error. Theorists have been trying to construct a formal mathematical model of the shape of the universe. In formal terms, this is a 3-manifold model corresponding to the spatial section (in comoving coordinates) of the 4-dimensional space-time of the universe. The model most theorists currently use is the so-called Friedmann–Lemaître–Robertson–Walker (FLRW) model. Arguments have been put forward that the observational data best fit with the conclusion that the shape of the global universe is infinite and flat, but the data are also consistent with other possible shapes, such as the so-called Poincaré dodecahedral space and the Picard horn.