Download Document

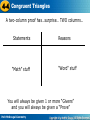
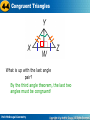
Triangles
4-4
Congruent
Triangles
4-4 Congruent
Warm Up
Lesson Presentation
Lesson Quiz
Holt
HoltGeometry
McDougal Geometry
4-4 Congruent Triangles
Warm Up
1. Name all sides and angles of ∆FGH.
FG, GH, FH, F, G, H
2. What is true about K and L? Why?
 ;Third s Thm.
3. What does it mean for two segments to
be congruent?
They have the same length.
Holt McDougal Geometry
4-4 Congruent Triangles
Objectives
Use properties of congruent triangles.
Prove triangles congruent by using the
definition of congruence.
Holt McDougal Geometry
4-4 Congruent Triangles
Geometric figures are congruent if they are the same
size and shape.
Corresponding angles and corresponding sides
are in the same position in polygons with an equal
number of sides.
Two polygons are congruent polygons if and only if
their corresponding sides are congruent.
Thus triangles that are the same size and shape are
congruent.
Holt McDougal Geometry
4-4 Congruent Triangles
Holt McDougal Geometry
4-4 Congruent Triangles
Helpful Hint
Two vertices that are the endpoints of a
side are called consecutive vertices.
For example, P and Q are consecutive
vertices. P and S are not.
P
Q
S
Holt McDougal Geometry
4-4 Congruent Triangles
To name a polygon, write the vertices
in consecutive order.
In a congruence statement, the order
of the vertices indicates the
corresponding parts.  so the order
MATTERS!
Holt McDougal Geometry
4-4 Congruent Triangles
Helpful Hint
When you write a statement such as
ABC  DEF, you are also stating
which parts are congruent.
Holt McDougal Geometry
4-4 Congruent Triangles
Example 1: Naming Congruent Corresponding Parts
Given: ∆PQR  ∆STW
Identify all pairs of corresponding congruent parts.
Angles: P  S, Q  T, R  W
Sides: PQ  ST, QR  TW, PR  SW
Holt McDougal Geometry
4-4 Congruent Triangles
Example 2A: Using Corresponding Parts of Congruent
Triangles
Given: ∆ABC  ∆DBC.
Find the value of x.
BCA and BCD are rt. s.
Def. of  lines.
BCA  BCD
Rt.   Thm.
mBCA = mBCD
Def. of  s
(2x – 16)° = 90°
2x = 106
x = 53
Holt McDougal Geometry
Substitute values for mBCA and
mBCD.
Add 16 to both sides.
Divide both sides by 2.
4-4 Congruent Triangles
Example 2B: Using Corresponding Parts of Congruent
Triangles
Given: ∆ABC  ∆DBC.
Find mDBC.
mABC + mBCA + mA = 180°∆ Sum Thm.
Substitute values for mBCA and
mABC + 90 + 49.3 = 180
mA.
mABC + 139.3 = 180 Simplify.
mABC = 40.7
DBC  ABC
Subtract 139.3 from both
sides.
Corr. s of  ∆s are  .
mDBC = mABC Def. of  s.
mDBC  40.7°
Holt McDougal Geometry
Trans. Prop. of =
4-4 Congruent Triangles
Check It Out! Example 2a
Given: ∆ABC  ∆DEF
Find the value of x.
AB  DE
Corr. sides of  ∆s are .
AB = DE
Def. of  parts.
2x – 2 = 6
2x = 8
x=4
Holt McDougal Geometry
Substitute values for AB and DE.
Add 2 to both sides.
Divide both sides by 2.
4-4 Congruent Triangles
Check It Out! Example 2b
Given: ∆ABC  ∆DEF
Find mF.
mEFD + mDEF + mFDE =
180°
ABC  DEF
Corr. s of  ∆ are .
mABC = mDEF
Def. of  s.
mDEF = 53°
Transitive Prop. of =.
mEFD + 53 + 90 = 180
mF + 143 = 180
mF = 37°
Holt McDougal Geometry
∆ Sum Thm.
Substitute values for mDEF
and mFDE.
Simplify.
Subtract 143 from both sides.
4-4 Congruent Triangles
Holt McDougal Geometry
4-4 Congruent Triangles
There are two ways to format proofs
Way 1: Two column proof
(this is the way we will do our proofs… College professors
everywhere will laugh at us, but we don’t care!)
Way 2: Paragraph proof
(You can choses to do you proofs this way and impress
the laughing college professors, but you don’t have to
succumb to their mockery.)
Holt McDougal Geometry
4-4 Congruent Triangles
A two-column proof has…surprise… TWO columns…
Statements
“Math” stuff
Reasons
“Word” stuff
You will always be given 1 or more “Givens”
and you will always be given a “Prove”
Holt McDougal Geometry
4-4 Congruent Triangles
In order to “prove” that two triangles are congruent,
what do we need…??
We must know that all corresponding
angles are congruent, and all
corresponding sides are congruent.
SO that is 6 things we need to put in our proof.
Holt McDougal Geometry
4-4 Congruent Triangles
Step 1: MARK IT UP!!!
Step 2: Decide what you are using
Step 3: ATTACK! Check off the use
Step 4: Get to the end goal, the PROVE
Holt McDougal Geometry
4-4 Congruent Triangles
Example 3: Proving Triangles Congruent
Given: YWX and YWZ are right angles.
YW bisects XYZ. W is the midpoint of XZ. XY  YZ.
Prove: ∆XYW  ∆ZYW
Start with step 1
Holt McDougal Geometry
4-4 Congruent Triangles
So lets talk about what we have marked up,
and what we do not have marked up.
HAVE
• 2 sides congruent
• 2 angles congruent
MISSING
• 1 side pair
• 1 angle pair
Holt McDougal Geometry
4-4 Congruent Triangles
What is up with the last side?
YW is the same in both triangles, therefore
it is congruent to itself!
This is the reflexive property.
We are going to use this A LOT
Holt McDougal Geometry
4-4 Congruent Triangles
What is up with the last angle
pair?
By the third angle theorem, the last two
angles must be congruent!
Holt McDougal Geometry
4-4 Congruent Triangles
• We officially have a reason for each side
being congruent and each angle being
congruent. Let’s pop it into our fancy
two-column proof.
Holt McDougal Geometry
4-4 Congruent Triangles
Statements
Reasons
1. YWX and YWZ are rt. s.
1. Given
2. YWX  YWZ
2. Rt.   Thm.
3. YW bisects XYZ
3. Given
4. XYW  ZYW
4. Def. of bisector
A
5. X  Z
5. Third s Thm.
A
6. W is midpoint. of XZ
6. Given
7. XW  ZW
7. Def. of midpoint
8. YW  YW
8. Reflex. Prop. of  S
9. XY  YZ
9. Given
10. ∆XYW  ∆ZYW
10. Def. of  ∆
Holt McDougal Geometry
A
S
S
4-4 Congruent Triangles
Check It Out! Example 3
Given: AD bisects BE.
BE bisects AD.
AB  DE, A  D
Prove: ∆ABC  ∆DEC
We are missing 2 angles this time.
ÐBCA @ ÐECD
ÐB @ ÐE
Holt McDougal Geometry
Because they are vertical angles.
By the third angle theorem.
4-4 Congruent Triangles
Statements
Reasons
1. A  D
1. Given
2. BCA  DCE
2. Vertical s are . A
3. ABC  DEC
3. Third s Thm.
A
4. AB  DE
4. Given
S
5. AD bisects BE,
5. Given
A
BE bisects AD
6. BC  EC, AC  DC
6. Def. of bisector
7. ∆ABC  ∆DEC
7. Def. of  ∆s
Holt McDougal Geometry
S S
4-4 Congruent Triangles
Lesson Quiz
1. ∆ABC  ∆JKL and AB = 2x + 12. JK = 4x – 50.
Find x and AB. 31, 74
Given that polygon MNOP  polygon QRST,
identify the congruent corresponding part.
RS
P
2. NO  ____
3. T  ____
4. Given: C is the midpoint of BD and AE.
A  E, AB  ED
Prove: ∆ABC  ∆EDC
Holt McDougal Geometry
4-4 Congruent Triangles
Lesson Quiz
4.
Statements
Reasons
1. A  E
1. Given
2. C is mdpt. of BD and AE
2. Given
3. AC  EC; BC  DC
3. Def. of mdpt.
4. AB  ED
4. Given
5. ACB  ECD
5. Vert. s Thm.
6. B  D
6. Third s Thm.
7. ABC  EDC
7. Def. of  ∆s
Holt McDougal Geometry