Visualizing Hyperbolic Geometry
... A straight line segment can be drawn joining any two points. A straight line segment can be extended indefinitely in a straight line. Given any straight line segment, a circle can be drawn having the segment as a radius and one endpoint as center. All right angles are congruent. If two lines are dra ...
... A straight line segment can be drawn joining any two points. A straight line segment can be extended indefinitely in a straight line. Given any straight line segment, a circle can be drawn having the segment as a radius and one endpoint as center. All right angles are congruent. If two lines are dra ...
4-5
... Two congruent angle pairs are give, but the included sides are not given as congruent. Therefore ASA cannot be used to prove the triangles congruent. Holt Geometry ...
... Two congruent angle pairs are give, but the included sides are not given as congruent. Therefore ASA cannot be used to prove the triangles congruent. Holt Geometry ...
Using Inductive Reasoning to Make Conjectures Bellringer
... Example 2B: Making a Conjecture Complete the conjecture. The number of lines formed by 4 points, no three of which are collinear, is ? . ...
... Example 2B: Making a Conjecture Complete the conjecture. The number of lines formed by 4 points, no three of which are collinear, is ? . ...
Holt McDougal Geometry
... 1. m1 = 120°, m2 = (60x)° Alt. Ext. s Thm.; m2 = 120° 2. m2 = (75x – 30)°, m3 = (30x + 60)° Corr. s Post.; m2 = 120°, m3 = 120° 3. m3 = (50x + 20)°, m4= (100x – 80)° Alt. Int. s Thm.; m3 = 120°, m4 =120° 4. m3 = (45x + 30)°, m5 = (25x + 10)° Same-Side Int. s Thm.; m3 = 120°, m5 =6 ...
... 1. m1 = 120°, m2 = (60x)° Alt. Ext. s Thm.; m2 = 120° 2. m2 = (75x – 30)°, m3 = (30x + 60)° Corr. s Post.; m2 = 120°, m3 = 120° 3. m3 = (50x + 20)°, m4= (100x – 80)° Alt. Int. s Thm.; m3 = 120°, m4 =120° 4. m3 = (45x + 30)°, m5 = (25x + 10)° Same-Side Int. s Thm.; m3 = 120°, m5 =6 ...
Geometer`s Sketchpad and the New Geometry Strands
... Instructions Sample Activities Key Curriculum Press (some are free) Mathbits Library of Resources from the Math Forum ...
... Instructions Sample Activities Key Curriculum Press (some are free) Mathbits Library of Resources from the Math Forum ...
Congruent
... • 2. Carefully read the problem and mark the diagram. • 3. Place a question mark (?) in the area that you need to prove. • 4. Create a flow diagram. • 5. Use one given at a time and draw as much information as possible from that given. • (Disregard information that is not needed.) • 6. Sequentially ...
... • 2. Carefully read the problem and mark the diagram. • 3. Place a question mark (?) in the area that you need to prove. • 4. Create a flow diagram. • 5. Use one given at a time and draw as much information as possible from that given. • (Disregard information that is not needed.) • 6. Sequentially ...
Holt McDougal Geometry 4-6
... to the diagram, the triangles are right triangles and one pair of legs is congruent. You do not know that one hypotenuse is congruent to the other. ...
... to the diagram, the triangles are right triangles and one pair of legs is congruent. You do not know that one hypotenuse is congruent to the other. ...
Chapter 16 - BISD Moodle
... •30. Both curves cannot correspond to lines. (Lines are great circles and great circles divide the sphere into two equal hemispheres. If one of these curves divides the sphere into two equal hemispheres, the other one clearly does not.) Euclidean and Sphere Geometries. •31. One. •32. No. 33. That th ...
... •30. Both curves cannot correspond to lines. (Lines are great circles and great circles divide the sphere into two equal hemispheres. If one of these curves divides the sphere into two equal hemispheres, the other one clearly does not.) Euclidean and Sphere Geometries. •31. One. •32. No. 33. That th ...
triangle
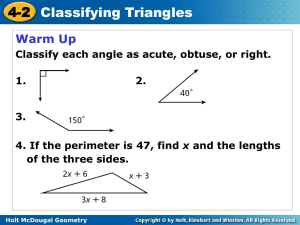
... Classify triangles by their angle measures and side lengths. Use triangle classification to find angle measures and side lengths. ...
... Classify triangles by their angle measures and side lengths. Use triangle classification to find angle measures and side lengths. ...
Math Review Large Print (18 point) Edition Chapter 3: Geometry
... plane figures, such as angles, triangles, other polygons, and circles. The terms “point,” “line,” and “plane” are familiar intuitive concepts. A point has no size and is the simplest geometric figure. All geometric figures consist of points. A line is understood to be a straight line that extends in ...
... plane figures, such as angles, triangles, other polygons, and circles. The terms “point,” “line,” and “plane” are familiar intuitive concepts. A point has no size and is the simplest geometric figure. All geometric figures consist of points. A line is understood to be a straight line that extends in ...
G6-3-Conditions for Paralleograms
... always a parallelogram? Since the bolt is at the midpoint of both legs, PE = ER and SE = EQ. So the diagonals of PQRS bisect each other, and by Theorem 6-3-5, PQRS is always a parallelogram. ...
... always a parallelogram? Since the bolt is at the midpoint of both legs, PE = ER and SE = EQ. So the diagonals of PQRS bisect each other, and by Theorem 6-3-5, PQRS is always a parallelogram. ...
6-3
... Since the bolt is at the midpoint of both legs, PE = ER and SE = EQ. So the diagonals of PQRS bisect each other, and by Theorem 6-3-5, PQRS is always a parallelogram. ...
... Since the bolt is at the midpoint of both legs, PE = ER and SE = EQ. So the diagonals of PQRS bisect each other, and by Theorem 6-3-5, PQRS is always a parallelogram. ...
Good Similar Polygons power point
... have two sizes of paper for your printer: 4 × 6 and 5 × 7. Does it matter? Will the pictures printed from each size of paper be similar? ...
... have two sizes of paper for your printer: 4 × 6 and 5 × 7. Does it matter? Will the pictures printed from each size of paper be similar? ...
Slide 1 - Nutley Public Schools
... The positions of the longest and shortest sides of a triangle are related to the positions of the largest and smallest angles. ...
... The positions of the longest and shortest sides of a triangle are related to the positions of the largest and smallest angles. ...
EPH-classifications in Geometry, Algebra, Analysis and Arithmetic
... (n − 1)-manifold and the closed half-ray. The manifold is of finite volume if and only if its thick part is compact. For n > 2 the hyperbolic structure on a finite volume hyperbolic n-manifold is unique by Mostow rigidity and so geometric invariants are in fact topological invariants. The geometries ...
... (n − 1)-manifold and the closed half-ray. The manifold is of finite volume if and only if its thick part is compact. For n > 2 the hyperbolic structure on a finite volume hyperbolic n-manifold is unique by Mostow rigidity and so geometric invariants are in fact topological invariants. The geometries ...
1-3 Measuring and Constructing Angles
... A transit is a tool for measuring angles. It consists of a telescope that swivels horizontally and vertically. Using a transit, a survey or can measure the angle formed by his or her location and two distant points. An angle is a figure formed by two rays, or sides, with a common endpoint called the ...
... A transit is a tool for measuring angles. It consists of a telescope that swivels horizontally and vertically. Using a transit, a survey or can measure the angle formed by his or her location and two distant points. An angle is a figure formed by two rays, or sides, with a common endpoint called the ...
1-3
... A transit is a tool for measuring angles. It consists of a telescope that swivels horizontally and vertically. Using a transit, a survey or can measure the angle formed by his or her location and two distant points. An angle is a figure formed by two rays, or sides, with a common endpoint called the ...
... A transit is a tool for measuring angles. It consists of a telescope that swivels horizontally and vertically. Using a transit, a survey or can measure the angle formed by his or her location and two distant points. An angle is a figure formed by two rays, or sides, with a common endpoint called the ...
1-3
... A transit is a tool for measuring angles. It consists of a telescope that swivels horizontally and vertically. Using a transit, a survey or can measure the angle formed by his or her location and two distant points. An angle is a figure formed by two rays, or sides, with a common endpoint called the ...
... A transit is a tool for measuring angles. It consists of a telescope that swivels horizontally and vertically. Using a transit, a survey or can measure the angle formed by his or her location and two distant points. An angle is a figure formed by two rays, or sides, with a common endpoint called the ...
Shape of the universe

The shape of the universe is the local and global geometry of the Universe, in terms of both curvature and topology (though, strictly speaking, the concept goes beyond both). The shape of the universe is related to general relativity which describes how spacetime is curved and bent by mass and energy.There is a distinction between the observable universe and the global universe. The observable universe consists of the part of the universe that can, in principle, be observed due to the finite speed of light and the age of the universe. The observable universe is understood as a sphere around the Earth extending 93 billion light years (8.8 *1026 meters) and would be similar at any observing point (assuming the universe is indeed isotropic, as it appears to be from our vantage point).According to the book Our Mathematical Universe, the shape of the global universe can be explained with three categories: Finite or infinite Flat (no curvature), open (negative curvature) or closed (positive curvature) Connectivity, how the universe is put together, i.e., simply connected space or multiply connected.There are certain logical connections among these properties. For example, a universe with positive curvature is necessarily finite. Although it is usually assumed in the literature that a flat or negatively curved universe is infinite, this need not be the case if the topology is not the trivial one.The exact shape is still a matter of debate in physical cosmology, but experimental data from various, independent sources (WMAP, BOOMERanG and Planck for example) confirm that the observable universe is flat with only a 0.4% margin of error. Theorists have been trying to construct a formal mathematical model of the shape of the universe. In formal terms, this is a 3-manifold model corresponding to the spatial section (in comoving coordinates) of the 4-dimensional space-time of the universe. The model most theorists currently use is the so-called Friedmann–Lemaître–Robertson–Walker (FLRW) model. Arguments have been put forward that the observational data best fit with the conclusion that the shape of the global universe is infinite and flat, but the data are also consistent with other possible shapes, such as the so-called Poincaré dodecahedral space and the Picard horn.