Download Algebra I - Denise Kapler

Agenda
I know
?
Lines and Angles
An angle is formed by two rays that
share a common endpoint
How do you form a line
from two rays?
Word Opposite rays
October 2014
Agenda
I know
?
Geometry
That Euclidean Geometry is
logic base.
Logic - reason
What is reason?
Word Definitions and Postulates
September 2014
Agenda
I
Geometry
That Euclidean Geometry provides an
know organized structure for deducing
knowledge. This structure through
accepted undefined terms, definitions,
and postulates provided certainty of
truth in its findings for many millennia.
? What is truth?
Word Truth = fidelity
September 2014
Agenda
I
Geometry
Polygons are many sided shapes.
Quadrilaterals
are
polygons
with
four
know
sides: including Parallelogram,
Trapezoid, Rectangle, Rhombus and
Square. To determine which one you
need to know angle and side length
measures and/or slope.
?
How can you tell what shape a
given figure is?
September 2014
Word Properties
Agenda
I
Euclidean Geometry
That Euclidean Geometry is based on
know definitions, undefined terms (point,
line and plane) and the 5 postulates of
the mathematician Euclid (330 BC)
? Why are there undefined terms?
Word
Undefined
September 2014
Agenda
I
Euclidean Geometry
That a point is defined by one
know coordinate (x) in 1-D; a line by (x,y)
in 2-D and a plane by (x,y,z) in 3-D.
?
How many coordinates define
space?
Word
Point, Line, Plane
September 2014
Agenda
I
Euclidean Geometry
That Euclidean Geometry is founded
know
on 5 basic postulates.
1. A straight line can be drawn between two points.
2. A straight line can be extended indefinitely.
3. A circle is defined by a point at its center and a radius extending from this
point
4. All right angles are congruent
5. Through a point not on a line, there is only one other line parallel to the line.
?
Do parallel lines ever touch?
Word Parallel
September 2014
Agenda
Euclidean Geometry
I
An angle is formed by two rays with a
know common vertex and that Euclidean
Geometry studies angle pairs that include:
1.
2.
3.
4.
5.
6.
Adjacent Angles – have the same vertex and share a common ray
Linear Pair - adjacent angles that sum to 180⁰
Vertical Angles – are congruent, formed by 2 intersecting lines
Complementary Angles – sum to 90⁰
Supplementary Angles – sum to 180⁰
Angles formed by transversals and parallel lines (will study later)
? What makes angles so powerful?
Word Angle Measure
September 2014
Agenda
I know
Euclidean Geometry
A parallax angle, formed by an angle
bisector, can be used to determine how far
away a “nearby” star is:
?Word How is the bisector formed?
Angle Bisector
September 2014
Agenda
Euclidean Geometry
I know
angles can be used to make indirect
measurements using shadows.
A student is standing next to a flagpole.
Shadows are cast by the sun.
?
What assumption is being made
about the light’s path?
Word Assumptions
September 2014
Agenda Reasoning – Logic Based Thinking
I know
?
reasoning is either
inductive or deductive
In your life,
when do you use reasoning?
Word
Reasoning - the process of thinking about
something in a logical way in order to form
a conclusion or judgment
September 2014
Agenda Reasoning – Logic Based Thinking
I know
?
inductive reasoning is used by
scientists when they form
hypotheses to test
In your life, when do you use
inductive reasoning?
Word
Inductive Reasoning – used to make
conjectures and to continue patterns
September 2014
Agenda Reasoning – Logic Based Thinking
I know deductive reasoning is the basis
for proof in math and law
?
In your life, when do you use
deductive reasoning?
Word
Deductive Reasoning – uses logic to
draw conclusions
September 2014
Math Review October 13, 2014
1. Find the area 2. What is the
and
relationship
circumference
between
∠1
of the circle
and
∠2?
If
r=7
∠1= 37⁰,
solve for ∠2.
1
2
A= bh A=s1+s2+s3
A=lw; P=2l+2w
A=πr2 C=2πr
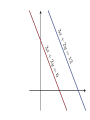
3. Graph the
following
system. What
is the
relationship
between the
two lines?
y= mx + b
defines linear
Math Review October 14, 2014
1. Find the area 2. What is the
and
relationship
circumference
between
∠1
of the circle
and
∠4?
If
r=5
∠1= 37⁰,
solve for ∠4.
3. Graph the
following
system. What
is the
relationship
between the
two lines?
{
1
2
A= bh A=s1+s2+s3
A=lw; P=2l+2w
A=πr2 C=2πr
y=x
y=-x
y= mx + b
defines linear
Math Review October 15, 2014
1. Find the area 2. What is the
and
relationship
circumference
between
∠1
of the circle
and
∠5?
r=1
Given l ⃦ m, if
∠1= 37⁰,
solve for ∠5.
3. Graph the
following
system. What
is the
relationship
between the
two lines?
{
1
2
A= bh A=s1+s2+s3
A=lw; P=2l+2w
A=πr2 C=2πr
y= 3x
y=- 1 x
3
y= mx + b
defines linear
Math Review September 3, 2014
1a. 225
If real: state if
rational or
irrational.
1b. Plot x > -3
on a number
line
2.
Find the distance
between
(4, -3) and (8, -6)
day 2
3. Plot the points
and find the
slope of the line
defined by:
(2, -6) and (-1, -8)
Distance Formula
m
Real numbers exist
on the number line
d
 y  y  x  x 
2
2
1
2
1
2
y 2  y1
x2  x1
y= mx + b
defines linear
Math Review September 4, 2014
1a. 625
If real: state if
rational or
irrational.
1b. Plot x ≥ -3
on a number
line
2.
Find the distance
between
(-2, 3) and (4, -5)
day 3
3. Plot the points
and find the
slope of the line
defined by:
(2, -6) and (-1, 0)
Distance Formula
m
Real numbers exist
on the number line
d
 y  y  x  x 
2
2
1
2
1
2
y 2  y1
x2  x1
y= mx + b
defines linear
Math Review September 5, 2014
1a. 196
If real: state if
rational or
irrational.
2. Find the
distance between
(-5, 1) and (1, -7)
3. Plot the points
and find the
slope of the line
defined by:
1b. Plot
10 < x < 100 on
a number line
Real numbers exist
on the number line
(4, -1) and (4, 3)
m
d
 y  y  x  x 
2
2
1
2
1
2
y 2  y1
x2  x1
y= mx + b
defines linear
Math Review September 8, 2014
1a. 169
If real: state if
rational or
irrational.
2. Find the
distance between
(-5, 24) and (2, 0)
3. Write the
equation of the
line defined by:
(2, -4) and (-1, 2)
1b. Plot
-8 < x ≤ 3 on a
number line
Real numbers exist
on the number line
day7
d
 y  y  x  x 
2
2
1
2
1
2
Write the line
equation in
slope intercept
form.
y= mx + b
defines linear
Math Review September 9, 2014
1a.
3
If real: state if
rational or
irrational.
2. Find the
distance between
(-4, 22) and (3, -2)
3. Write the
equation of the
line defined by:
(1, 3) and (-1, 3)
1b. Plot
-8 ≤ x < 3 on a
number line
Real numbers exist
on the number line
day 8
Write the line
equation in
slope intercept
form.
d
 y  y  x  x 
2
2
1
2
1
2
y= mx + b
defines linear
Math Review September 10, 2014
1a. 2
If real: state if
rational or
irrational.
2. Find the
distance between
(-6, 2) and (2, -4)
3. Write the
equation of the
line defined by:
(4, -4) and (4, -1)
1b. Plot
-0.2 < x < 0.3
on a number
line
Real numbers exist
on the number line
day 5
Write the line
equation in
slope intercept
form.
d
 y  y  x  x 
2
2
1
2
1
2
y= mx + b
defines linear
Math Review September 11, 2014
1a. 400
If real: state if
rational or
irrational.
2. Find the
distance between
(-5, 24) and (2, 0)
3. Write the
equation of the
line defined by:
(3, -2) and (-4, 5)
1b. Plot
-10 < x <-1 on
a number line
Real numbers exist
on the number line
Write the line
equation in
slope intercept
form.
d
 y  y  x  x 
2
2
1
2
1
2
y= mx + b
defines linear
Math Review September 15, 2014
1a. Determine
area of square
with side
lengths of 2”
1b. Determine
perimeter of
square with
side lengths of
2”
Area = lw
Perimeter= 2l + 2w
3. Graph y= 1
2. Find the
x
midpoint between
(-6, 24) and (2, 0)
Name its function
family
y= mx + b
defines linear
Math Review September 16, 2014
1a. Determine
area of a
figure: square
of side length
2’ with a half
circle on top.
1b. Determine
its perimeter
Area = lw
Perimeter= 2l + 2w
A =  r2
C = 2 r
3. Graph y=
2. Find the
midpoint between
(-5, 63) and (-1, 1)
x
Name its function
family
y= mx + b
defines linear
Math Review September 17, 2014
1a. Determine
area of a figure
comprised of:
3” radius circle
with a square of
side length 1”
cut out from its
center
1b. Determine its
perimeter
Area = lw
Perimeter= 2l + 2w
A =  r2
C = 2 r
3. Graph y = x2
2. Find the
midpoint between
(1, -1) and (1, -1)
Name its function
family
y= mx + b
defines linear
Math Review September 18, 2014
1a. Determine
area of the
figure
1b. Determine its
perimeter 4’
3’
3. Graph
2. Find the
2 + 2x +1
f(x)
=
x
midpoint between
(5, -8) and (-1, 1)
3’
3’
Area = lw
Perimter= 2l + 2w
A =  r2
C = 2 r
Name its function
family
y= mx + b
defines linear
Math Review September 22, 2014
1a. Determine
area of blue
part of circle
r= 4cm
1b. Determine its
perimeter
2. Solve for x.
Give algebraic
reasons for
each step.
2x + 3 = 21
3. Graph
f(x) = -x2
Name its function
family
Area = lw
Perimeter= 2l + 2w
A =  r2
C = 2 r
Given
Properties of Real Numbers
1. Equality Under Operations:
reflective, symmetric and
transitive
2. Equality: Substitution
3. Simplify (Arithmetic)
y= mx + b
defines linear
Math Review September 23, 2014
1a. Determine
area of blue
circle r= 2cm
when circle with
r=1cm is cut out
1b. Determine its
perimeter
Area = lw
Perimeter= 2l + 2w
A =  r2
C = 2 r
2. 2. Solve for x.
Give algebraic
reasons for
each step.
5x + 7 = 22
3. Graph
f(x) = x2
Name its function
family
Given
Properties of Real Numbers
1. Equality Under Operations:
reflective, symmetric and
transitive
2. Equality: Substitution
3. Simplify (Arithmetic)
y= mx + b
defines linear
Math Review September 24, 2014
1a. Determine
area of the blue
figure r= 1cm
1b. Determine its
perimeter
2. 2. Solve for x.
Give algebraic
reasons for
each step.
5x + 17 = 22x
3. Graph
f(x) = 2x
Name its function
family
Area = lw
Perimeter= 2l + 2w
A =  r2
C = 2 r
Given
Properties of Real Numbers
1. Equality Under Operations:
reflective, symmetric and
transitive
2. Equality: Substitution
3. Simplify (Arithmetic)
y= mx + b
defines linear
Math Review September 25, 2014
1a. Determine
area of
equilateral
triangle s= 1cm
1b. Determine its
perimeter
2. 2. Solve for x.
Give algebraic
reasons for
each step.
6x + 7 = 22 - 3
3. Graph
f(x) = -2x
Name its function
family
Area = lw
Perimeter= 2l + 2w
A =  r2
C = 2 r
Given
Properties of Real Numbers
1. Equality Under Operations:
reflective, symmetric and
transitive
2. Equality: Substitution
3. Simplify (Arithmetic)
y= mx + b
defines linear
Agenda
I know
Algebra
That a system of equation’s
solution is found at the point of
intersection.
?
How do you know if two lines are
parallel, perpendicular or neither?
Word Parallel
Perpendicular
September 2014
Agenda
I
Algebra
That the Pythagorean Theorem
know
works when I have a right triangle.
?
How do you find a right angle
in the real world?
Word Right angle = 90°
September 2014
Agenda
I know
?
Algebra
That the Pythagorean Theorem is
used to solve real life problems.
When can I assume a right
angles exists?
Word
2-dimension
September 2014
Agenda
I know
?
Algebra
That the Pythagorean Theorem can
be used to find the side length of a
right triangle.
How can you tell if a triangle is
a right triangle?
Word
a^2 + b^2 = c^2
September 2014
1a.
Math Review September 2014
2. Find the
distance
between (-5, 2)
and (1,-2)
-4 = - (3m+1)
1b.
2u+2v+u=
2v+2u+u
1c.
-x+(3x+2)=
(-x+3x)+2
Properties of Real
numbers:
Associative,
Commutative and
Distributive.
d
 y  y  x  x 
2
2
1
2
1
2
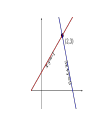
3. Plot the points
and find the
slope defined
by:
Line 1
(0, 2) and (2,-2)
Line 2
(10, 2) and (2,-2)
Do the lines
intersect?
y= mx + b
defines linear
Agenda
I know
?
Algebra
That the Line of Best Fit for a
scatterplot has the same number
of points above as below it.
Why is the Line of Best Fit an
average?
Word
points
September
Math Review
1a.
2. Find the
distance
between (-5, 3)
and (10,-5)
-11 = - (5m+1)
1b.
u+v+10u=
v+u+10u
1c.
3. Plot the points
and find the
slope defined
by:
Line 1:
(2, 2) and (2,-2)
Line 2:
(2, 2) and (-2,2)
-2x+(x+2)=
(-2x+x)+2
Properties of Real
numbers:
Associative,
Commutative and
Distributive.
d
 y  y  x  x 
2
2
1
2
1
2
m
y 2  y1
x2  x1
y= mx + b
defines linear
1a.
Math Review April 16, 2014
3. Plot the points
2. Find the
and find the
distance
slope defined
between (-5, 33)
by:
and (4,-7)
8 = - (3y+9)
1b.
2a+2b+a=
2b+2a+a
1c.
Line 1
(7, -2) and (-1,-2)
Line 2
(-1,-2) and (7, -2)
6x+(4x+8)=
(6x+4x)+8
Properties of Real
numbers:
Associative,
Commutative and
Distributive.
d
 y  y  x  x 
2
2
1
2
1
2
Do the lines
intersect?
y= mx + b
defines linear
Agenda
I know
?
Algebra
That a scatterplot has a line of best
that is linear when the data has an
average a constant rate of change.
Why is the Line of Best Fit a
straight line?
Word
Average
September
1a.
Math Review April 17, 2014
3. Plot the points
2. Find the
and find the
distance
slope defined
between (-5, 33)
by:
and (4,-7)
8 = - (3y+9)
1b.
2a+2b+a=
2b+2a+a
1c.
Line 1
(1, 0) and (-2,6)
Line 2
(0, 0) and (3,-6)
6x+(4x+8)=
(6x+4x)+8
Properties of Real
numbers:
Associative,
Commutative and
Distributive.
d
 y  y  x  x 
2
2
1
2
1
2
Do the lines
intersect?
y= mx + b
defines linear
Agenda
Algebra
I know That a scatterplot provides a
summary of the data points.
?
How do you draw a
Line of Best Fit?
Word
Line of Best Fit
September
Agenda
Geometry
I know How to analyze the pattern in an
algebraic relationship using:
tables, graphs and equations.
?
How do you find the common
ratio in a geometric sequence?
Word
September
Agenda
I know
?
Geometry
How to analyze the pattern in an
algebraic relationship using:
changes in y.
How do you find the common
difference/slope in an algebraic
sequence?
Word m =
September
Agenda
Geometry
I know the distance formula will find the
distance between two points.
?
How do you find the distance
between two points?
Word
d
x  x 
2
1
2

y  y 
2
1
2
September
d
 y  y x  x 
2
1
2
1
Math Review
1a.
a+(b+c)=(a+b)+c 2a. Find the
distance
between (3, 4)
and (0,0)
1b.
a+b +c=b+a+c
1c.
2b. Solve for c.
a=4 and b=3
3. Plot the points,
draw the line
and find the
equation
defined by:
(-3, 5) and (0, 2)
2(x+1)=10
Properties of
2
2 y= mx + b
Real numbers:
d  y  y   x 2  x1
2
1
defines linear
Associative,
Commutative
a2+b2=c2
and Distributive.


Math Review
1a.
-(2x+2)=16
3. Plot the points,
draw the line
and find the
equation
defined by:
2. Find the
distance
between (-4, 3)
and (0,0)
1b.
9x+y+3x=
y+9x+3x
2b. Solve for c.
1c.
(-2, 4) and (1, 1)
a=3 and b=4
5x+(4x+3)=
(5x+4x)+3
Properties of Real
numbers:
Associative,
Commutative and
Distributive.
d
 y  y  x  x 
2
2
a2+b2=c2
1
2
1
2
y= mx + b
defines linear
Math Review
1a.
3(2x+2)=18
2. Find the
distance
1b.
between (2, 3)
x+3y+5x=
and (-6, 9)
3y+x+5x
2b. Solve for c.
1c.
a=6 and b=8
7x+(3x+1)=
(7x+3x)+1
Properties of Real
numbers:
Associative,
Commutative and
Distributive.
d
3. Plot the points,
draw the line
and find the
equation
defined by:
(-2, -4) and (2, 4)
 y  y  x  x 
2
2
a2+b2=c2
1
2
1
2
y= mx + b
defines linear
1a.
-7(2x+2)=28
1b.
7x+y+x=
y+7x+x
1c.
2a+(a+9)=
(2a+a)+9
Properties of Real
numbers:
Associative,
Commutative and
Distributive.
Math Review
2a. Find the
distance between
(-6, 3) and (6,-2)
3. Plot the points,
draw the line
and find the
equation
defined by:
2b. Solve for c.
a=5 and b=12
d
(5, 3) and (-1, -3)
 y  y  x  x 
2
2
1
a2+b2=c2
2
1
2
y= mx + b
defines linear
Solve Steps
Word Problems
1.
2.
3.
4.
5.
6.
Draw – picture, graph, table
Known- from inside and outside the problem
Unknown – what are you being asked to find
Relationship – between known and unknown
Solve
Answer: Does it make sense? Plug it back in
Solve Steps
1.
2.
3.
Use GEMDAS - work one side then the
other
Isolate the variable - when there is
nothing left to do on either side
Use one variable to solve for the other(s)
- for a system
Solve Steps
1.
2.
3.
Read and write down the problem
Ask yourself - What do I do next?
Think - about what you know
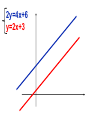
2y=4x+6
y=2x+3
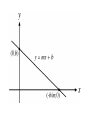
Agenda
Linear Functions
I know the slope intercept form
defines linear.
?
Word
Why do linear equations graph a
straight line?
Change in y
Change in x
11-14-2012
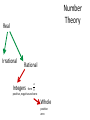
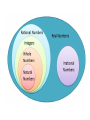
Number
Theory
Real
Irrational
Rational
a
form b
positive, negative and zero
Integers
Whole
positive
zero
Set of Real Numbers
Agenda
Real Number Operations
I know Multiplication is repeated addition;
Division repeated subtraction
?
What are the four things you can
do to a number?
Word
Inverse
9-10-2012
Decimal – place value
Y-intercept
X-intercept
•Find the y-intercept by setting x to
zero and solving for y.
•Find the x-intercept by setting y to
zero and solving for x
Notebook
Organizer Notes from class
Notes from class
Date
Title
Happy Mole Day!!!!