to word - Warner School of Education
... rings, and fields, and the relationship between these structures and formal structures for number systems and numerical and symbolic calculations NCTM 2012 1.A.2.7 History of Algebra Historical development and perspectives of algebra including contributions of significant figures and diverse culture ...
... rings, and fields, and the relationship between these structures and formal structures for number systems and numerical and symbolic calculations NCTM 2012 1.A.2.7 History of Algebra Historical development and perspectives of algebra including contributions of significant figures and diverse culture ...
lecture12-orig - School of Computer Science
... might just be a “one-way” function Multiplication is fast to compute Reverse multiplication is apparently slow We have a feasible method to multiply 1000 bit numbers [Egyptian multiplication] Factoring the product of two random 1000 bit primes has no known feasible approach. ...
... might just be a “one-way” function Multiplication is fast to compute Reverse multiplication is apparently slow We have a feasible method to multiply 1000 bit numbers [Egyptian multiplication] Factoring the product of two random 1000 bit primes has no known feasible approach. ...
- Triumph Learning
... Perimeter and Area . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86 ...
... Perimeter and Area . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86 ...
The Mathematics of Harmony: Clarifying the Origins and
... “Science had been the life blood and sustenance of mathematics. Mathematicians were willing partners with physicists, astronomers, chemists, and engineers in the scientific enterprise. In fact, during the 17th and 18th centuries and most of the 19th, the distinction between mathematics and theoretic ...
... “Science had been the life blood and sustenance of mathematics. Mathematicians were willing partners with physicists, astronomers, chemists, and engineers in the scientific enterprise. In fact, during the 17th and 18th centuries and most of the 19th, the distinction between mathematics and theoretic ...
Continuum Hypothesis, Axiom of Choice, and Non-Cantorian Theory
... Any infinite sequence of distinct numbers has CardN . This Axiom establishes Cantorian Cardinality. The Effective Countability Axiom guarantees that sequencing is sufficient to establish equal Cantorian cardinalities. All sequences have the same cardinality as the sequence of the natural numbers. Si ...
... Any infinite sequence of distinct numbers has CardN . This Axiom establishes Cantorian Cardinality. The Effective Countability Axiom guarantees that sequencing is sufficient to establish equal Cantorian cardinalities. All sequences have the same cardinality as the sequence of the natural numbers. Si ...
Ninth and Tenth Grades Knowledge Base Indicators
... a. a recursive or explicit formula for arithmetic sequences and finds any particular term, b. a recursive or explicit formula for geometric sequences and finds any particular term. Application Indicators The student… 1. recognizes the same general pattern presented in different representations [nume ...
... a. a recursive or explicit formula for arithmetic sequences and finds any particular term, b. a recursive or explicit formula for geometric sequences and finds any particular term. Application Indicators The student… 1. recognizes the same general pattern presented in different representations [nume ...
Section 1.1
... describe patterns of your own. Sometimes, patterns allow you to make accurate predictions. ...
... describe patterns of your own. Sometimes, patterns allow you to make accurate predictions. ...
Math - KVS RO
... History, Repeated experiments and observed frequency approach to probability. Focus is on empirical probability. (A large amount of time to be devoted to group and to individual activities to motivate the concept; the experiments to be drawn from real - life situations, and from examples used in the ...
... History, Repeated experiments and observed frequency approach to probability. Focus is on empirical probability. (A large amount of time to be devoted to group and to individual activities to motivate the concept; the experiments to be drawn from real - life situations, and from examples used in the ...
Multiple Choice
... 15. Doc and Marty were studying what happens when a fair spinner is spun a large number of times. Marty predicted that they would probably get more “big” number s than small since they were experimenting late in the month. Doc tried to say that a fair spinner will land on all numbers approximately t ...
... 15. Doc and Marty were studying what happens when a fair spinner is spun a large number of times. Marty predicted that they would probably get more “big” number s than small since they were experimenting late in the month. Doc tried to say that a fair spinner will land on all numbers approximately t ...
Algebra I - Denise Kapler
... That Euclidean Geometry is based on know definitions, undefined terms (point, line and plane) and the 5 postulates of the mathematician Euclid (330 BC) ...
... That Euclidean Geometry is based on know definitions, undefined terms (point, line and plane) and the 5 postulates of the mathematician Euclid (330 BC) ...
Unit 10: Reflections and Symmetry
... 10 highlights a return to geometry from the point of view of transformations or “motions” of geometric figures. It focuses primarily ...
... 10 highlights a return to geometry from the point of view of transformations or “motions” of geometric figures. It focuses primarily ...
Maths Foundation Revision
... whole GCSE which includes topics learned in year 7 and topics that you will be learning after January. ...
... whole GCSE which includes topics learned in year 7 and topics that you will be learning after January. ...
Abelian and non-Abelian numbers via 3D Origami
... the real roots of any polynomial of degree n and coefficients in Z using (n − 2)-fold axioms. In turn every real algebraic number can be reached. 1.3. New 3D folding axioms. In this work we propose new folding axioms that, added to the HJAs, allow us to construct new numbers. The new ingredient we p ...
... the real roots of any polynomial of degree n and coefficients in Z using (n − 2)-fold axioms. In turn every real algebraic number can be reached. 1.3. New 3D folding axioms. In this work we propose new folding axioms that, added to the HJAs, allow us to construct new numbers. The new ingredient we p ...
Keys GEO SY14-15 Openers 3-10
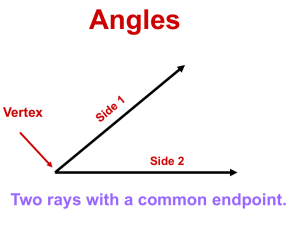
... Corresponding Angles transversal, then each pair of CO Corresponding Angles/|| Lines so that each pair of CO s is , Postulate (CO s Post.) s is . Postulate (CO s/|| Lines Post.) then the lines are ||. Theorem 3.1 If 2 || lines are cut by a Theorem 3.5 If 2 lines are cut by a transversal so Alt ...
... Corresponding Angles transversal, then each pair of CO Corresponding Angles/|| Lines so that each pair of CO s is , Postulate (CO s Post.) s is . Postulate (CO s/|| Lines Post.) then the lines are ||. Theorem 3.1 If 2 || lines are cut by a Theorem 3.5 If 2 lines are cut by a transversal so Alt ...
It`s Rare Disease Day!!! Happy Birthday nylon, Ben Hecht, Linus
... If 2 lines are cut by a transversal so that each pair of CI s is supplementary, then the lines are ||. If 2 lines are cut by a transversal so that each pair of AI s is , then the lines are ||. If you have 1 line and 1 point NOT on that line, ONE and only ONE line goes through that point that’s || ...
... If 2 lines are cut by a transversal so that each pair of CI s is supplementary, then the lines are ||. If 2 lines are cut by a transversal so that each pair of AI s is , then the lines are ||. If you have 1 line and 1 point NOT on that line, ONE and only ONE line goes through that point that’s || ...
Keys GEO Openers 4-15
... 2 s are if 2 sides and the included angle of EAT BUN one are to the corresponding 2 sides and included angle of another . 2 s are if 2 angles and the included side of FAT FLY 1 are to 2 corresponding angles and the included side of the other . 2 s are if 2 angles and a non ...
... 2 s are if 2 sides and the included angle of EAT BUN one are to the corresponding 2 sides and included angle of another . 2 s are if 2 angles and the included side of FAT FLY 1 are to 2 corresponding angles and the included side of the other . 2 s are if 2 angles and a non ...
KEY
... Definition: A counterexample is an example that justifies that a statement is false. Example 1: The numbers of days in every month is 31. A counterexample is February, since it only has 28 days. Another counter example is April, it only has 30 days. Example 2: For any integer n, n < 4n. A counterexa ...
... Definition: A counterexample is an example that justifies that a statement is false. Example 1: The numbers of days in every month is 31. A counterexample is February, since it only has 28 days. Another counter example is April, it only has 30 days. Example 2: For any integer n, n < 4n. A counterexa ...
Keys GEO SY14-15 Openers 3-13
... Corresponding Angles transversal, then each pair of CO Corresponding Angles/|| Lines so that each pair of CO s is , Postulate (CO s Post.) s is . Postulate (CO s/|| Lines Post.) then the lines are ||. Theorem 3.1 If 2 || lines are cut by a Theorem 3.5 If 2 lines are cut by a transversal so Alt ...
... Corresponding Angles transversal, then each pair of CO Corresponding Angles/|| Lines so that each pair of CO s is , Postulate (CO s Post.) s is . Postulate (CO s/|| Lines Post.) then the lines are ||. Theorem 3.1 If 2 || lines are cut by a Theorem 3.5 If 2 lines are cut by a transversal so Alt ...
Co-ordinate Geometry
... (B,2)or (4, 2) [See Fig. 191 (ii))]. The pair of numbers used for coding is called ordered pair. If we know the coding of a particular city, roughly we can indicate it’s location inside the shaded square on the map. But still we do not know its precise location. The method of finding the , position ...
... (B,2)or (4, 2) [See Fig. 191 (ii))]. The pair of numbers used for coding is called ordered pair. If we know the coding of a particular city, roughly we can indicate it’s location inside the shaded square on the map. But still we do not know its precise location. The method of finding the , position ...
Algebra I - Denise Kapler
... That Euclidean Geometry is based on know definitions, undefined terms (point, line and plane) and the 5 postulates of the mathematician Euclid (330 BC) ...
... That Euclidean Geometry is based on know definitions, undefined terms (point, line and plane) and the 5 postulates of the mathematician Euclid (330 BC) ...
Axioms and Theorems
... uncovered. And since these can’t be together, they cannot be covered by one domino. Therefore it is impossible. ...
... uncovered. And since these can’t be together, they cannot be covered by one domino. Therefore it is impossible. ...