No Slide Title - Cloudfront.net
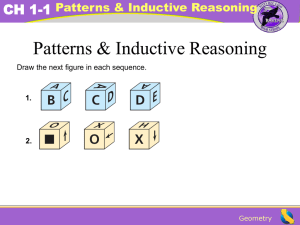
... The number of lines formed by 4 points, no three of which are collinear, is ? . Draw four points. Make sure no three points are collinear. Count the number of lines formed: ...
... The number of lines formed by 4 points, no three of which are collinear, is ? . Draw four points. Make sure no three points are collinear. Count the number of lines formed: ...
What is Math - Houston Independent School District
... At the end of the tournament, all players except the final winner will have lost exactly one match. In each match there is exactly one looser. Therefore, the number of matches equals the number of players excluding the final winner. Suppose the tournament has n participants. Then, n-1 matches will b ...
... At the end of the tournament, all players except the final winner will have lost exactly one match. In each match there is exactly one looser. Therefore, the number of matches equals the number of players excluding the final winner. Suppose the tournament has n participants. Then, n-1 matches will b ...
Numbers, proof and `all that jazz`.
... only our axioms. In fact, in these notes, we usually adopt a much looser standard. As the reader will see, proving everything directly from the axioms would take so long that we would never progress beyond this section! It is, however, important that the reader prove a number of basic number facts u ...
... only our axioms. In fact, in these notes, we usually adopt a much looser standard. As the reader will see, proving everything directly from the axioms would take so long that we would never progress beyond this section! It is, however, important that the reader prove a number of basic number facts u ...
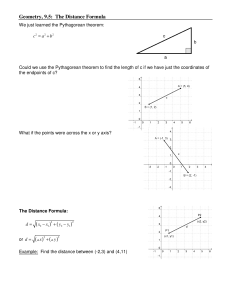
Geometry, 9.5: The Distance Formula
... Procedure for using Pythagorean triples to find a missing side: 1) Find a number that divides evenly into the 2 sides given. 2) Divide both sides by that number and write new side lengths in parentheses. 3) Match new sides to a Pythagorean triple and fill in missing side. 4) Make a proportion with t ...
... Procedure for using Pythagorean triples to find a missing side: 1) Find a number that divides evenly into the 2 sides given. 2) Divide both sides by that number and write new side lengths in parentheses. 3) Match new sides to a Pythagorean triple and fill in missing side. 4) Make a proportion with t ...
Geometry of Flat Surfaces
... for d = 2 we have ν2 = 0 for d = 3 we have ν2 = 0 for d = 4 we have ν2 = 1/3 for d = 5 we have ν2 = 1/2 (all rational...) for d = 6 we have ν2 = 0, 6156 . . . or 0, 7173 . . . (probably irrational...) Conjecture (Kontsevich-Zorich). The sum ν1 + ν2 + · · · + νg is a rational number for all g ≥ 3. ...
... for d = 2 we have ν2 = 0 for d = 3 we have ν2 = 0 for d = 4 we have ν2 = 1/3 for d = 5 we have ν2 = 1/2 (all rational...) for d = 6 we have ν2 = 0, 6156 . . . or 0, 7173 . . . (probably irrational...) Conjecture (Kontsevich-Zorich). The sum ν1 + ν2 + · · · + νg is a rational number for all g ≥ 3. ...
Axioms and Theorems
... Proving that the domino problem is impossible. Therefore the first 30 dominoes (wherever they are put) must cover 30 white squares and 30 black. This MUST leave two black squares uncovered. And since these can’t be together, they cannot be covered by one domino. Therefore it is impossible. ...
... Proving that the domino problem is impossible. Therefore the first 30 dominoes (wherever they are put) must cover 30 white squares and 30 black. This MUST leave two black squares uncovered. And since these can’t be together, they cannot be covered by one domino. Therefore it is impossible. ...
AMC 10 Student Practice Questions
... NCTM Standard: Geometry Standard: explore relationships (including congruence and similarity) among classes of two- and three-dimensional geometric objects, make and test conjectures about Difficulty: Medium-hard them, and solve problems involving them. explore relationships (including congruence an ...
... NCTM Standard: Geometry Standard: explore relationships (including congruence and similarity) among classes of two- and three-dimensional geometric objects, make and test conjectures about Difficulty: Medium-hard them, and solve problems involving them. explore relationships (including congruence an ...
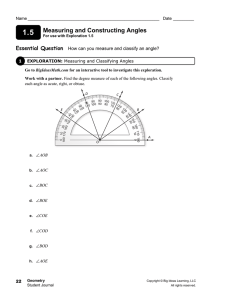
Measuring and Constructing Angles
... Work with a partner. Find the degree measure of each of the following angles. Classify each angle as acute, right, or obtuse. ...
... Work with a partner. Find the degree measure of each of the following angles. Classify each angle as acute, right, or obtuse. ...
CHAP02 Axioms of Set Theory
... We need the Axiom of Infinity to get an infinite set and with the Axiom of Specification we can be sure that subclasses of sets are indeed subsets. The Axiom of Substitution is rather more technical than the others, but in essence it says that any class that is in 1-1 correspondence with s set is a ...
... We need the Axiom of Infinity to get an infinite set and with the Axiom of Specification we can be sure that subclasses of sets are indeed subsets. The Axiom of Substitution is rather more technical than the others, but in essence it says that any class that is in 1-1 correspondence with s set is a ...
7-2 - MrsFaulkSaysMathMatters
... 1. By the Isosc. ∆ Thm., A C, so by the def. of , mC = mA. Thus mC = 70° by subst. By the ∆ Sum Thm., mB = 40°. Apply the Isosc. ∆ Thm. and the ∆ Sum Thm. to ∆PQR. mR = mP = 70°. So by the def. of , A P, and C R. Therefore ∆ABC ~ ∆PQR by AA ~. ...
... 1. By the Isosc. ∆ Thm., A C, so by the def. of , mC = mA. Thus mC = 70° by subst. By the ∆ Sum Thm., mB = 40°. Apply the Isosc. ∆ Thm. and the ∆ Sum Thm. to ∆PQR. mR = mP = 70°. So by the def. of , A P, and C R. Therefore ∆ABC ~ ∆PQR by AA ~. ...
Document
... Elliptic curves and number theory Roughly, an elliptic curve over a field F is the graph of an equation of the form y 2 p( x ) where p(x) is a cubic polynomial with three distinct roots and coefficients in F. The fields of most interest are the rational numbers, finite fields, the real numbers, a ...
... Elliptic curves and number theory Roughly, an elliptic curve over a field F is the graph of an equation of the form y 2 p( x ) where p(x) is a cubic polynomial with three distinct roots and coefficients in F. The fields of most interest are the rational numbers, finite fields, the real numbers, a ...
Copyright © by Holt, Rinehart and Winston
... Show that each conjecture is false by finding a counterexample. 8. If three lines lie in the same plane, then they intersect in at least one point. ________________________________________________________________________________________ ...
... Show that each conjecture is false by finding a counterexample. 8. If three lines lie in the same plane, then they intersect in at least one point. ________________________________________________________________________________________ ...
Document
... Elliptic curves and number theory Roughly, an elliptic curve over a field F is the graph of an equation of the form y 2 p( x ) where p(x) is a cubic polynomial with three distinct roots and coefficients in F. The fields of most interest are the rational numbers, finite fields, the real numbers, a ...
... Elliptic curves and number theory Roughly, an elliptic curve over a field F is the graph of an equation of the form y 2 p( x ) where p(x) is a cubic polynomial with three distinct roots and coefficients in F. The fields of most interest are the rational numbers, finite fields, the real numbers, a ...
Geometry Chapter 1 Review Use inductive reasoning to find the next
... Geometry Chapter 1 Review Use inductive reasoning to find the next two numbers in each pattern. ...
... Geometry Chapter 1 Review Use inductive reasoning to find the next two numbers in each pattern. ...
Use inductive reasoning to find the next two numbers in each pattern
... Geometry Chapter 1 Review Use inductive reasoning to find the next two numbers in each pattern. ...
... Geometry Chapter 1 Review Use inductive reasoning to find the next two numbers in each pattern. ...
geometric mean
... Find the geometric mean of each pair of numbers. If necessary, give the answer in simplest radical form. 6 and 15 Let x be the geometric mean. ...
... Find the geometric mean of each pair of numbers. If necessary, give the answer in simplest radical form. 6 and 15 Let x be the geometric mean. ...
Mathematical Ideas that Shaped the World
... numbers than whole numbers! The infinity of the whole numbers is called “countable”, while the infinity of the real numbers is called “uncountable”. In fact, there are infinitely many sizes of ...
... numbers than whole numbers! The infinity of the whole numbers is called “countable”, while the infinity of the real numbers is called “uncountable”. In fact, there are infinitely many sizes of ...
Meet 3 Cat 2 SG
... 1. Imagine taking a walk counter-clockwise around the regular decagon. You will make ten left-hand turns of the same measure. When you get back to where you started, you will have turned a total of 360 degrees. Therefore, each exterior angle must be 360 ÷ 10 = 36 degrees. ...
... 1. Imagine taking a walk counter-clockwise around the regular decagon. You will make ten left-hand turns of the same measure. When you get back to where you started, you will have turned a total of 360 degrees. Therefore, each exterior angle must be 360 ÷ 10 = 36 degrees. ...
Geometric Mean PowerPoint
... Find the geometric mean of each pair of numbers. If necessary, give the answer in simplest radical form. 6 and 15 Let x be the geometric mean. ...
... Find the geometric mean of each pair of numbers. If necessary, give the answer in simplest radical form. 6 and 15 Let x be the geometric mean. ...
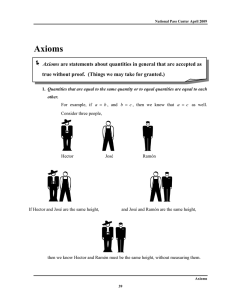
Axioms - Geneseo Migrant Center
... 8. If equals are added or subtracted from unequals or if unequals are multiplied or divided by the same positive number, the results are unequal in that same order. This axiom is the same as Axioms 2, 3, and 4, except that now we start with two things that are not equal. Say, 12 < 36 . This axiom st ...
... 8. If equals are added or subtracted from unequals or if unequals are multiplied or divided by the same positive number, the results are unequal in that same order. This axiom is the same as Axioms 2, 3, and 4, except that now we start with two things that are not equal. Say, 12 < 36 . This axiom st ...
Lecture 10. Axioms and theories, more examples. Axiomatic
... Reading: Chapter 8: 8.5, Chapter 9: 9.1 – 9.4 of PtMW, pp. 206 –211, 247- 253. ...
... Reading: Chapter 8: 8.5, Chapter 9: 9.1 – 9.4 of PtMW, pp. 206 –211, 247- 253. ...
Section 3
... 3.2 Checking group axioms So far we have considered sets of symmetries of plane figures. These give a large number of examples of groups, many of which are finite. In the audio section we consider how the group axioms apply (or do not apply) in other situations. Another source of examples of groups is ...
... 3.2 Checking group axioms So far we have considered sets of symmetries of plane figures. These give a large number of examples of groups, many of which are finite. In the audio section we consider how the group axioms apply (or do not apply) in other situations. Another source of examples of groups is ...
Essential Defenses Secondary
... The negation of a statement such as "All birds fly" is roughly formed by saying, "It is false that 'all birds fly.'" These rules also apply: Rule 1: If a statement is true, its negation must be false. Rule 2: If a statement is false, its negation must be true. Below is a table of four statements tha ...
... The negation of a statement such as "All birds fly" is roughly formed by saying, "It is false that 'all birds fly.'" These rules also apply: Rule 1: If a statement is true, its negation must be false. Rule 2: If a statement is false, its negation must be true. Below is a table of four statements tha ...
Inductive Reasoning and Patterns
... afternoon, Natalie told Imari to go home and study her Geometry notes. Why? ...
... afternoon, Natalie told Imari to go home and study her Geometry notes. Why? ...
Final Jeopardy - Queen Anne's County Public Schools / Overview
... ►x00xx0000xxx000000______ ►x0x0x0x0x0x0x0_________ ► What ...
... ►x00xx0000xxx000000______ ►x0x0x0x0x0x0x0_________ ► What ...