Download 7-2 - MrsFaulkSaysMathMatters

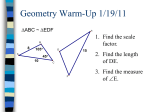
7-1
7-1 Ratio
Ratioand
andProportion
Proportion
Warm Up
Lesson Presentation
Lesson Quiz
Holt
Geometry
Holt
Geometry
7-1 Ratio and Proportion
Objectives
Write and simplify ratios.
Use proportions to solve problems.
Holt Geometry
7-1 Ratio and Proportion
A ratio compares two numbers by division. The ratio
of two numbers a and b can be written as a to b, a:b,
or
, where b ≠ 0. For example, the ratios 1 to 2,
1:2, and
all represent the same comparison.
Remember!
In a ratio, the denominator of the fraction cannot be
zero because division by zero is undefined.
Holt Geometry
7-1 Ratio and Proportion
A ratio can involve more than two numbers. For
the rectangle, the ratio of the side lengths may
be written as 3:7:3:7.
Holt Geometry
7-1 Ratio and Proportion
Example 2: Using Ratios
The ratio of the side lengths of a triangle is
4:7:5, and its perimeter is 96 cm. What is the
length of the shortest side?
Let the side lengths be 4x, 7x, and 5x.
Then 4x + 7x + 5x = 96 . After like terms are
combined, 16x = 96. So x = 6. The length of the
shortest side is 4x = 4(6) = 24 cm.
Holt Geometry
7-1 Ratio and Proportion
Check It Out! Example 2
The ratio of the angle measures in a triangle is
1:6:13. What is the measure of each angle?
x + y + z = 180°
x + 6x + 13x = 180°
20x = 180°
x = 9°
y = 6x
z = 13x
y = 6(9°)
z = 13(9°)
y = 54°
z = 117°
Holt Geometry
7-1 Ratio and Proportion
A proportion is an equation stating that two ratios
are equal. In the proportion
, the values
a and d are the extremes. The values b and c
are the means. When the proportion is written as
a:b = c:d, the extremes are in the first and last
positions. The means are in the two middle positions.
Holt Geometry
7-1 Ratio and Proportion
In Algebra 1 you learned the Cross Products
Property. The product of the extremes ad and the
product of the means bc are called the cross
products.
Reading Math
The Cross Products Property can also be stated
as, “In a proportion, the product of the extremes
is equal to the product of the means.”
Holt Geometry
7-1 Ratio and Proportion
The following table shows equivalent forms of the
Cross Products Property.
Holt Geometry
7-1 Ratio and Proportion
Page 6
Holt Geometry
7-2
7-2 Ratios
RatiosininSimilar
SimilarPolygons
Polygons
Warm Up
Lesson Presentation
Lesson Quiz
Holt
Geometry
Holt
Geometry
7-2 Ratios in Similar Polygons
Objectives
Identify similar polygons.
Apply properties of similar polygons to
solve problems.
Vocabulary
similar
similar polygons
similarity ratio
Holt Geometry
7-2 Ratios in Similar Polygons
Figures that are similar (~) have the same shape
but not necessarily the same size.
Holt Geometry
7-2 Ratios in Similar Polygons
Two polygons are
similar polygons if
and only if their
corresponding
angles are
congruent and their
corresponding side
lengths are
proportional.
Holt Geometry
7-2 Ratios in Similar Polygons
Example 1: Describing Similar Polygons
Identify the pairs of
congruent angles and
corresponding sides.
N  Q and P  R.
By the Third Angles Theorem, M  T.
Holt Geometry
0.5
7-2 Ratios in Similar Polygons
Check It Out! Example 1
Identify the pairs of
congruent angles and
corresponding sides.
B  G and C  H.
By the Third Angles Theorem, A  J.
Holt Geometry
7-2 Ratios in Similar Polygons
A similarity ratio is the ratio of the lengths of
the corresponding sides of two similar polygons.
The similarity ratio of ∆ABC to ∆DEF is
, or
The similarity ratio of ∆DEF to ∆ABC is
, or 2.
Holt Geometry
.
7-2 Ratios in Similar Polygons
Writing Math
Writing a similarity statement is like writing a
congruence statement—be sure to list
corresponding vertices in the same order.
Helpful Hint
When you work with proportions, be sure the
ratios compare corresponding measures.
Holt Geometry
7-2 Ratios in Similar Polygons
Example 2A: Identifying Similar Polygons
Determine whether the polygons are similar.
If so, write the similarity ratio and a
similarity statement.
rectangles ABCD and EFGH
Holt Geometry
7-2 Ratios in Similar Polygons
Example 2A Continued
Step 1 Identify pairs of congruent angles.
A  E, B  F,
C  G, and D  H.
All s of a rect. are rt. s
and are .
Step 2 Compare corresponding sides.
Thus the similarity ratio is
Holt Geometry
, and rect. ABCD ~ rect. EFGH.
7-2 Ratios in Similar Polygons
Example 2B: Identifying Similar Polygons
Determine whether the
polygons are similar. If
so, write the similarity
ratio and a similarity
statement.
∆ABCD and ∆EFGH
Holt Geometry
7-2 Ratios in Similar Polygons
Example 2B Continued
Step 1 Identify pairs of congruent angles.
P  R and S  W
isos. ∆
Step 2 Compare corresponding angles.
mW = mS = 62°
mT = 180° – 2(62°) = 56°
Since no pairs of angles are congruent, the triangles
are not similar.
Holt Geometry
7-2 Ratios in Similar Polygons
Check It Out! Example 2
Determine if ∆JLM ~ ∆NPS.
If so, write the similarity
ratio and a similarity
statement.
Step 1 Identify pairs of congruent angles.
N  M, L  P, S  J
Holt Geometry
7-2 Ratios in Similar Polygons
Check It Out! Example 2 Continued
Step 2 Compare corresponding sides.
Thus the similarity ratio is
Holt Geometry
, and ∆LMJ ~ ∆PNS.
7-2 Ratios in Similar Polygons
Holt Geometry
7-2 Ratios in Similar Polygons
Holt Geometry
7-2 Ratios in Similar Polygons
Holt Geometry
7-2 Ratios in Similar Polygons
Lesson Quiz: Part I
1. Determine whether the polygons are similar. If so,
write the similarity ratio and a similarity
statement.
no
2. The ratio of a model sailboat’s dimensions to the
actual boat’s dimensions is . If the length of the
model is 10 inches, what is the length of the
actual sailboat in feet?
25 ft
Holt Geometry
7-2 Ratios in Similar Polygons
Lesson Quiz: Part II
3. Tell whether the following statement is
sometimes, always, or never true. Two equilateral
triangles are similar.
Always
Holt Geometry
Triangle
Similarity:
7-3
7-3 Triangle Similarity: AA, SSS, and SAS
AA, SSS, and SAS
Warm Up
Lesson Presentation
Lesson Quiz
Holt
Geometry
Holt
Geometry
7-3 Triangle Similarity: AA, SSS, and SAS
Objectives
Prove certain triangles are similar by
using AA, SSS, and SAS.
Use triangle similarity to solve problems.
Holt Geometry
7-3 Triangle Similarity: AA, SSS, and SAS
There are several ways to prove certain triangles are
similar. The following postulate, as well as the SSS
and SAS Similarity Theorems, will be used in proofs
just as SSS, SAS, ASA, HL, and AAS were used to
prove triangles congruent.
Holt Geometry
7-3 Triangle Similarity: AA, SSS, and SAS
Example 1: Using the AA Similarity Postulate
Explain why the triangles
are similar and write a
similarity statement.
Since
, B  E by the Alternate Interior
Angles Theorem. Also, A  D by the Right Angle
Congruence Theorem. Therefore ∆ABC ~ ∆DEC by
AA~.
Holt Geometry
7-3 Triangle Similarity: AA, SSS, and SAS
Check It Out! Example 1
Explain why the triangles
are similar and write a
similarity statement.
By the Triangle Sum Theorem, mC = 47°, so C  F.
B  E by the Right Angle Congruence Theorem.
Therefore, ∆ABC ~ ∆DEF by AA ~.
Holt Geometry
7-3 Triangle Similarity: AA, SSS, and SAS
Holt Geometry
7-3 Triangle Similarity: AA, SSS, and SAS
Holt Geometry
7-3 Triangle Similarity: AA, SSS, and SAS
Example 2A: Verifying Triangle Similarity
Verify that the triangles are similar.
∆PQR and ∆STU
Therefore ∆PQR ~ ∆STU by SSS ~.
Holt Geometry
7-3 Triangle Similarity: AA, SSS, and SAS
Example 2B: Verifying Triangle Similarity
Verify that the triangles are similar.
∆DEF and ∆HJK
D  H by the Definition of Congruent Angles.
Therefore ∆DEF ~ ∆HJK by SAS ~.
Holt Geometry
7-3 Triangle Similarity: AA, SSS, and SAS
Check It Out! Example 2
Verify that ∆TXU ~ ∆VXW.
TXU  VXW by the
Vertical Angles Theorem.
Therefore ∆TXU ~ ∆VXW by SAS ~.
Holt Geometry
7-3 Triangle Similarity: AA, SSS, and SAS
Example 3: Finding Lengths in Similar Triangles
Explain why ∆ABE ~ ∆ACD, and
then find CD.
Step 1 Prove triangles are similar.
A  A by Reflexive Property of , and B  C
since they are both right angles.
Therefore ∆ABE ~ ∆ACD by AA ~.
Holt Geometry
7-3 Triangle Similarity: AA, SSS, and SAS
Example 3 Continued
Step 2 Find CD.
Corr. sides are proportional.
Seg. Add. Postulate.
x(9) = 5(3 + 9)
9x = 60
Substitute x for CD, 5 for BE,
3 for CB, and 9 for BA.
Cross Products Prop.
Simplify.
Divide both sides by 9.
Holt Geometry
7-3 Triangle Similarity: AA, SSS, and SAS
Check It Out! Example 3
Explain why ∆RSV ~ ∆RTU
and then find RT.
Step 1 Prove triangles are similar.
It is given that S  T.
R  R by Reflexive Property of .
Therefore ∆RSV ~ ∆RTU by AA ~.
Holt Geometry
7-3 Triangle Similarity: AA, SSS, and SAS
Check It Out! Example 3 Continued
Step 2 Find RT.
Corr. sides are proportional.
Substitute RS for 10, 12 for
TU, 8 for SV.
RT(8) = 10(12) Cross Products Prop.
8RT = 120
RT = 15
Holt Geometry
Simplify.
Divide both sides by 8.
7-3 Triangle Similarity: AA, SSS, and SAS
Example 4: Writing Proofs with Similar Triangles
Given: 3UT = 5RT and 3VT = 5ST
Prove: ∆UVT ~ ∆RST
Holt Geometry
7-3 Triangle Similarity: AA, SSS, and SAS
Example 4 Continued
Statements
Reasons
1. 3UT = 5RT
1. Given
2.
2. Divide both sides by 3RT.
3. 3VT = 5ST
3. Given.
4.
4. Divide both sides by3ST.
5. RTS  VTU
5. Vert. s Thm.
6. ∆UVT ~ ∆RST
6. SAS ~
Holt Geometry
Steps 2, 4, 5
7-3 Triangle Similarity: AA, SSS, and SAS
Check It Out! Example 4
Given: M is the midpoint of JK. N is the
midpoint of KL, and P is the midpoint of JL.
Holt Geometry
7-3 Triangle Similarity: AA, SSS, and SAS
Check It Out! Example 4 Continued
Statements
Reasons
1. M is the mdpt. of JK,
N is the mdpt. of KL,
and P is the mdpt. of JL.
1. Given
2.
2. ∆ Midsegs. Thm
3.
3. Div. Prop. of =.
4. ∆JKL ~ ∆NPM
4. SSS ~ Step 3
Holt Geometry
7-3 Triangle Similarity: AA, SSS, and SAS
You learned in Chapter 2 that the Reflexive,
Symmetric, and Transitive Properties of Equality
have corresponding properties of congruence.
These properties also hold true for similarity of
triangles.
Holt Geometry
7-3 Triangle Similarity: AA, SSS, and SAS
Lesson Quiz
1. Explain why the triangles are
similar and write a similarity
statement.
2. Explain why the triangles are
similar, then find BE and CD.
Holt Geometry
7-3 Triangle Similarity: AA, SSS, and SAS
Lesson Quiz
1. By the Isosc. ∆ Thm., A  C, so by the def.
of , mC = mA. Thus mC = 70° by subst.
By the ∆ Sum Thm., mB = 40°. Apply the
Isosc. ∆ Thm. and the ∆ Sum Thm. to ∆PQR.
mR = mP = 70°. So by the def. of , A  P,
and C  R. Therefore ∆ABC ~ ∆PQR by AA ~.
2. A  A by the Reflex. Prop. of . Since BE ||
CD, ABE  ACD by the Corr. s Post.
Therefore ∆ABE ~ ∆ACD by AA ~. BE = 4 and
CD = 10.
Holt Geometry