- Triumph Learning
... Factors and Multiples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 ...
... Factors and Multiples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 ...
to word - Warner School of Education
... rings, and fields, and the relationship between these structures and formal structures for number systems and numerical and symbolic calculations NCTM 2012 1.A.2.7 History of Algebra Historical development and perspectives of algebra including contributions of significant figures and diverse culture ...
... rings, and fields, and the relationship between these structures and formal structures for number systems and numerical and symbolic calculations NCTM 2012 1.A.2.7 History of Algebra Historical development and perspectives of algebra including contributions of significant figures and diverse culture ...
Unit 10 - Georgia Standards
... • Understand that the basic properties of numbers continue to hold with polynomials During the school-age years, students must repeatedly extend their conception of numbers. From counting numbers to fractions, students are continually updating their use and knowledge of numbers. In Grade 8, students ...
... • Understand that the basic properties of numbers continue to hold with polynomials During the school-age years, students must repeatedly extend their conception of numbers. From counting numbers to fractions, students are continually updating their use and knowledge of numbers. In Grade 8, students ...
Ninth and Tenth Grades Knowledge Base Indicators
... a. a recursive or explicit formula for arithmetic sequences and finds any particular term, b. a recursive or explicit formula for geometric sequences and finds any particular term. Application Indicators The student… 1. recognizes the same general pattern presented in different representations [nume ...
... a. a recursive or explicit formula for arithmetic sequences and finds any particular term, b. a recursive or explicit formula for geometric sequences and finds any particular term. Application Indicators The student… 1. recognizes the same general pattern presented in different representations [nume ...
Co-ordinate Geometry
... In general, co-ordinates of a point P(x, y) imply that distance of P from the y-axis is x units and its distance from the x-axis is y units. You may note that the co-ordinates of the origin O are (0, 0). The y co-ordinate of every point on the x-axis is 0 and the x co-ordinate of every point on the ...
... In general, co-ordinates of a point P(x, y) imply that distance of P from the y-axis is x units and its distance from the x-axis is y units. You may note that the co-ordinates of the origin O are (0, 0). The y co-ordinate of every point on the x-axis is 0 and the x co-ordinate of every point on the ...
No Slide Title - Cloudfront.net
... The number of lines formed by 4 points, no three of which are collinear, is ? . Draw four points. Make sure no three points are collinear. Count the number of lines formed: ...
... The number of lines formed by 4 points, no three of which are collinear, is ? . Draw four points. Make sure no three points are collinear. Count the number of lines formed: ...
Geometry of Flat Surfaces
... Translation surfaces The flat surfaces obtained from planar polygons have some additional structure: a globally defined "compass". ...
... Translation surfaces The flat surfaces obtained from planar polygons have some additional structure: a globally defined "compass". ...
7-2 - MrsFaulkSaysMathMatters
... of , mC = mA. Thus mC = 70° by subst. By the ∆ Sum Thm., mB = 40°. Apply the Isosc. ∆ Thm. and the ∆ Sum Thm. to ∆PQR. mR = mP = 70°. So by the def. of , A P, and C R. Therefore ∆ABC ~ ∆PQR by AA ~. ...
... of , mC = mA. Thus mC = 70° by subst. By the ∆ Sum Thm., mB = 40°. Apply the Isosc. ∆ Thm. and the ∆ Sum Thm. to ∆PQR. mR = mP = 70°. So by the def. of , A P, and C R. Therefore ∆ABC ~ ∆PQR by AA ~. ...
Curriculum Map - Delaware City Schools
... a. estimating lengths using string or links, areas using tiles or grid,and volumes using cubes; b. measuring attributes (diameter, side lengths, or heights) and using established formulas for circles, triangles, rectangles, parallelograms and rectangular prisms. Geometry 3.D.1-Classify and describe ...
... a. estimating lengths using string or links, areas using tiles or grid,and volumes using cubes; b. measuring attributes (diameter, side lengths, or heights) and using established formulas for circles, triangles, rectangles, parallelograms and rectangular prisms. Geometry 3.D.1-Classify and describe ...
AMC 10 Student Practice Questions
... NCTM Standard: Geometry Standard: explore relationships (including congruence and similarity) among classes of two- and three-dimensional geometric objects, make and test conjectures about Difficulty: Medium-hard them, and solve problems involving them. explore relationships (including congruence an ...
... NCTM Standard: Geometry Standard: explore relationships (including congruence and similarity) among classes of two- and three-dimensional geometric objects, make and test conjectures about Difficulty: Medium-hard them, and solve problems involving them. explore relationships (including congruence an ...
A scout troop buys 1000 candy bars at a price of five for $2. They sell
... Since 99(a2 − b2 ) must be a perfect square, a2 − b2 = (a + b)(a − b) = 11k 2 , for some positive integer k. Because a and b are distinct digits, we have a − b ≤ 9 − 1 = 8 and a + b ≤ 9 + 8 = 17. It follows that a + b = 11, a − b = k 2 , and k is either 1 or 2. If k = 2, then (a, b) = (15/2, 7/2), w ...
... Since 99(a2 − b2 ) must be a perfect square, a2 − b2 = (a + b)(a − b) = 11k 2 , for some positive integer k. Because a and b are distinct digits, we have a − b ≤ 9 − 1 = 8 and a + b ≤ 9 + 8 = 17. It follows that a + b = 11, a − b = k 2 , and k is either 1 or 2. If k = 2, then (a, b) = (15/2, 7/2), w ...
Document
... Elliptic curves and number theory Roughly, an elliptic curve over a field F is the graph of an equation of the form y 2 p( x ) where p(x) is a cubic polynomial with three distinct roots and coefficients in F. The fields of most interest are the rational numbers, finite fields, the real numbers, a ...
... Elliptic curves and number theory Roughly, an elliptic curve over a field F is the graph of an equation of the form y 2 p( x ) where p(x) is a cubic polynomial with three distinct roots and coefficients in F. The fields of most interest are the rational numbers, finite fields, the real numbers, a ...
Similar Right Triangles
... Name _________________________________________________________ Date _________ ...
... Name _________________________________________________________ Date _________ ...
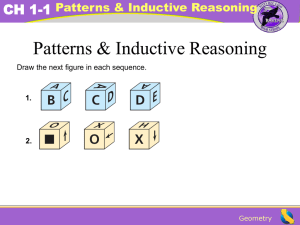
PH_Geo_1-1_Patterns_and_Inductive_Reasoning[1]
... – 3, 5, 7, ___ – One would think that the rule is add 2, but that gives us 9 for the fourth prime number. Is that true? – What is the next odd prime number? ...
... – 3, 5, 7, ___ – One would think that the rule is add 2, but that gives us 9 for the fourth prime number. Is that true? – What is the next odd prime number? ...
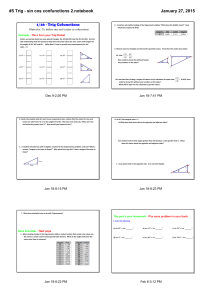
5 Trig - sin cos confunctions 2.notebook
... side relationships that we learned to determine the exact values for sine, cosine and tangent for the angles of 30°, 60° and 45°. (Why didn’t I have to provide any measurements for the sides…..?) 3. Thomas sees two triangles on the board in geometry class. From those he makes two claims: ...
... side relationships that we learned to determine the exact values for sine, cosine and tangent for the angles of 30°, 60° and 45°. (Why didn’t I have to provide any measurements for the sides…..?) 3. Thomas sees two triangles on the board in geometry class. From those he makes two claims: ...
BEAUTIFUL THEOREMS OF GEOMETRY AS VAN AUBEL`S
... it’s not often presented in Japan. I therefore delved into its roots. It is introduced in the 1971 edition of the ‘ Comprehensive Dictionary of Geometry, Volume 1 ’, on page 296 as problem number 387, and two proofs?one using elementary geometry and the other using complex numbers?are included[2]. P ...
... it’s not often presented in Japan. I therefore delved into its roots. It is introduced in the 1971 edition of the ‘ Comprehensive Dictionary of Geometry, Volume 1 ’, on page 296 as problem number 387, and two proofs?one using elementary geometry and the other using complex numbers?are included[2]. P ...
Prentice Hall Mathematics: Algebra 2 Scope and Sequence
... 4.2.E.2 Use a variety of strategies to determine perimeter and area of plane figures and surface area and volume of 3D figures: Approximation of area using grids of different size, Finding which shape has minimal or maximal area, perimeter, volume, or surface area under given conditions using graphi ...
... 4.2.E.2 Use a variety of strategies to determine perimeter and area of plane figures and surface area and volume of 3D figures: Approximation of area using grids of different size, Finding which shape has minimal or maximal area, perimeter, volume, or surface area under given conditions using graphi ...
Geometry - Teacher Resource Center
... G.1.2. Compose two-dimensional shapes (rectangles, squares, trapezoids, triangles, halfcircles, and quarter-circles) or three-dimensional shapes (cubes, right rectangular prisms, right circular cones, and right circular cylinders) to create a composite shape, and compose new shapes from the composit ...
... G.1.2. Compose two-dimensional shapes (rectangles, squares, trapezoids, triangles, halfcircles, and quarter-circles) or three-dimensional shapes (cubes, right rectangular prisms, right circular cones, and right circular cylinders) to create a composite shape, and compose new shapes from the composit ...
Math Review
... Algebraic Simplification • Basic rules that can be used to simplify or rearrange formulas. • These are most useful when using variables in equations, but can also be useful with numbers too. ...
... Algebraic Simplification • Basic rules that can be used to simplify or rearrange formulas. • These are most useful when using variables in equations, but can also be useful with numbers too. ...
lesson 1.8
... Could you find the area of the border? Area entire square=area inner + area outer. Solve for outer. Postulate 1-9: If 2 figures are congruent, then their areas are equal Postulate 1-10: The area of a region is the sum of its non-overlapping parts. Exercise: Find area of an irregular shape. Separate ...
... Could you find the area of the border? Area entire square=area inner + area outer. Solve for outer. Postulate 1-9: If 2 figures are congruent, then their areas are equal Postulate 1-10: The area of a region is the sum of its non-overlapping parts. Exercise: Find area of an irregular shape. Separate ...
Honors Geometry - Glenbard East High School
... 3. You will be quizzed over this material towards the end of the first week of school. You will be given time to ask some questions prior to that quiz and do some review. 4. You may work ...
... 3. You will be quizzed over this material towards the end of the first week of school. You will be given time to ask some questions prior to that quiz and do some review. 4. You may work ...
syllabus for group `x` (technical) english
... 3. Antonyms and Synonyms 4. One word substitution 5. Correct usage of articles 6. Correct usage of Prepositions 7. Correct usage of adjectives-degrees of comparison 8. Correct usage of conjunctions 9. Correct usage of Nouns and Pronouns 10. Correct usage of numbers (Singular-Plural) 11. Words, which ...
... 3. Antonyms and Synonyms 4. One word substitution 5. Correct usage of articles 6. Correct usage of Prepositions 7. Correct usage of adjectives-degrees of comparison 8. Correct usage of conjunctions 9. Correct usage of Nouns and Pronouns 10. Correct usage of numbers (Singular-Plural) 11. Words, which ...
Geometry
Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. A mathematician who works in the field of geometry is called a geometer. Geometry arose independently in a number of early cultures as a body of practical knowledge concerning lengths, areas, and volumes, with elements of formal mathematical science emerging in the West as early as Thales (6th century BC). By the 3rd century BC, geometry was put into an axiomatic form by Euclid, whose treatment—Euclidean geometry—set a standard for many centuries to follow. Archimedes developed ingenious techniques for calculating areas and volumes, in many ways anticipating modern integral calculus. The field of astronomy, especially as it relates to mapping the positions of stars and planets on the celestial sphere and describing the relationship between movements of celestial bodies, served as an important source of geometric problems during the next one and a half millennia. In the classical world, both geometry and astronomy were considered to be part of the Quadrivium, a subset of the seven liberal arts considered essential for a free citizen to master.The introduction of coordinates by René Descartes and the concurrent developments of algebra marked a new stage for geometry, since geometric figures such as plane curves could now be represented analytically in the form of functions and equations. This played a key role in the emergence of infinitesimal calculus in the 17th century. Furthermore, the theory of perspective showed that there is more to geometry than just the metric properties of figures: perspective is the origin of projective geometry. The subject of geometry was further enriched by the study of the intrinsic structure of geometric objects that originated with Euler and Gauss and led to the creation of topology and differential geometry.In Euclid's time, there was no clear distinction between physical and geometrical space. Since the 19th-century discovery of non-Euclidean geometry, the concept of space has undergone a radical transformation and raised the question of which geometrical space best fits physical space.With the rise of formal mathematics in the 20th century, 'space' (whether 'point', 'line', or 'plane') lost its intuitive contents, so today one has to distinguish between physical space, geometrical spaces (in which 'space', 'point' etc. still have their intuitive meanings) and abstract spaces.Contemporary geometry considers manifolds, spaces that are considerably more abstract than the familiar Euclidean space, which they only approximately resemble at small scales. These spaces may be endowed with additional structure which allow one to speak about length. Modern geometry has many ties to physics as is exemplified by the links between pseudo-Riemannian geometry and general relativity. One of the youngest physical theories, string theory, is also very geometric in flavour.While the visual nature of geometry makes it initially more accessible than other mathematical areas such as algebra or number theory, geometric language is also used in contexts far removed from its traditional, Euclidean provenance (for example, in fractal geometry and algebraic geometry).













![PH_Geo_1-1_Patterns_and_Inductive_Reasoning[1]](http://s1.studyres.com/store/data/004561992_1-58ea9afa053964924acdb00561313e99-300x300.png)