Download Geometric Mean Notes

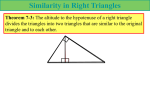
Discovering Geometry
Name:
CH. 11 NOTES: Geometric Mean And Similar Right Triangles
GEOMETRIC MEAN
A geometric sequence is one in which each consecutive number is found by multiplying the
previous number by a given factor. For example, suppose the first number of a sequence is 5
and the factor is 3. You can find the next four numbers in the sequence as shown below.
5  15  45  135  405
Consecutive numbers of the sequence form proportions.
5 15

15 45
15 45

45 135
45 135

135 405
Note that the denominator of one fraction is the numerator of the next. The GEOMETRIC
MEAN between two positive numbers a and b is the positive number where
a x
 . By cross
x b
multiplying, we see that x 2  ab or x  ab . Note that in the proportion, x and x represent the
MEANS and a and b represent the EXTREMES. (From Glencoe Geometry)
Examples of geometric mean:
1. Find the geometric mean between 4 and 25.
2. Find the geometric mean between 2 and 10.
You Try:
3. Find the geometric mean between 8 and 9.
4. Find the geometric mean between
1
2
and .
3
3
USING GEOMETRIC MEAN IN SIMILAR RIGHT TRIANGLES
If the altitude is drawn from the vertex of a right angle in a right triangle to its hypotenuse, then the
two smaller triangles formed are similar to the given bigger triangle and to each other.
N
Write the similarity statement for the 3 similar triangles.
20 70
S
ΔSNO ~ Δ
20
70
W
O
~Δ
Complete each statement.
A
a
B
75
15
ΔABC ~ Δ
b.
d b

b
c
b
75
15
D
d
a.
C
e
d.
d

~Δ
e

c de
c.
a
de
So, the measure of the altitude drawn from the vertex of the right angle of a right triangle to its
hypotenuse is the _________________ ______________ between the measures of
the 2 segments of the hypotenuse.
Also, the measure of a leg of the big right triangle is the _____________________
____________ between the measures of the hypotenuse and the segment of the
hypotenuse adjacent to that leg.
Apply Geometric Mean to Similar Right Triangles:
Find the value of each variable.
1.
2.
y
x
6
2
x
5
y
3
3.
4.
4
8
z
5
x
5
y
y
x
You Try:
Solve for the indicated variable.
5.
6.
x
x
18
y
15
6
x
7.
5
4x
16
8.
y
y
z
x
4
9.
9
10.
3
x
7
x
z
3
11.
24
12.
15
x
5
15
5
x