Download Exercises 8-1 - Spokane Public Schools

8-1
Exercises
8-1 Exercises
KEYWORD: MG7 8-1
KEYWORD: MG7 Parent
GUIDED PRACTICE
Assignment Guide
8
1. Vocabulary In the proportion __28 = __
, which number is the geometric mean of
32
the other two numbers? 8 is the geometric mean of 2 and 32.
SEE EXAMPLE
1
p. 518
Write a similarity statement comparing the three triangles in each diagram.
2.
3.
*
XYZ
∼ XWY
∼ YWZ
4. 8
7
,
SEE EXAMPLE
SEE EXAMPLE
+
-
BED ∼ ECD ∼ BCE
RPQ ∼ PSQ ∼ RSP
<
9
2
Find the geometric mean of each pair of numbers. If necessary, give the answer in
simplest radical form.
1 and 8 2
5. 2 and 50 10
6. 4 and 16 8
7. _
2
3
77
8. 9 and 12 6 √
9. 16 and 25 20
10. 7 and 11 √
3
Find x, y, and z.
p. 519
p. 520
11.
È
p. 520
12.
{
Þ
Ý
SEE EXAMPLE 4
Assign Guided Practice exercises
as necessary.
â
15 ;
2 √
2 √6;
2 √10
â
Þ
£ä
5; 10 √5; 13.
5 √
5
Þ
If you finished Examples 1–4
Basic 15–37, 41, 44, 47–49,
54–62
Average 15–27, 30–38 even,
39–50, 54–62
Advanced 15–27, 28–40 even,
42–62
ÈÊÊȖв
£ÎÊ
вÊ
Ý
Homework Quick Check
Ý
â
Óä
£n
13 ; 8
12; 4 √
14. Measurement To estimate the length of the
USS Constitution in Boston harbor, a student
locates points T and U as shown. What is RS
to the nearest tenth? 62.0 m
,
1
/
{ʓ
Èäʓ
PRACTICE AND PROBLEM SOLVING
Independent Practice
For
See
Exercises Example
15–17
18–23
24–26
27
1
2
3
4
Extra Practice
Skills Practice p. S18
Application Practice p. S35
Write a similarity statement comparing the three triangles in each diagram.
15. 16. +
RSU
∼ RTS
∼ STU
17. ,
/
*
MPN ∼ PQN ∼ MQP
If you finished Examples 1–2
Basic 15–23, 28, 29
Average 15–23, 28, 29, 45
Advanced 15–23, 28, 29, 45, 46
CAB ∼ ADB ∼ CDA
-
1
Quickly check key concepts.
Exercises: 16, 18, 24, 27, 36
Visual In Exercises 2–4
and 15–17, some students
may have difficulty visualizing the corresponding angles in the
overlapping triangles. Suggest that
they redraw the diagram to separate
the three triangles.
Inclusion Remind
students not to rely on the
given diagram for scale in
Exercises 14 and 27.
Find the geometric mean of each pair of numbers. If necessary, give the answer
in simplest radical form.
18. 5 and 45 15
1 and 80 2 √
5
21. _
4
10
20. 5 and 8 2 √
27
2
_
_
3 √
5
and
23.
3
40
5
19. 3 and 15 3 √
2
22. 1.5 and 12 3 √
_
10
Find x, y, and z.
24.
25.
{
£Ó
Þ
Ý
Ý
£Ó°n
â
Þ
â
32; 8 √2; 24 √
2
12; 16; 7.2
26.
Þ
™°È
Îä
â
{ä
20 √
3 ; 10 √
21 ; 20 √
7
Ý
8-1 Similarity in Right Triangles
ge07se_c08_0518_0523.indd 521
521
9/19/05 4:38:27 PM
KEYWORD: MG7 Resources
Lesson 8-1
521
Algebra Before
students begin Exercise
29, you may want to
review the properties of exponents.
2
2
That is, (a √x) = a 2( √
x ) = a 2x, for
x > 0.
27. Measurement To estimate the height of the Taipei 101
tower, Andrew stands so that his lines of sight to the top
and bottom of the tower form a 90° angle. What is the height
of the tower to the nearest foot? 1670 ft
91 ft 3 in.
28. The geometric mean of two numbers is 8. One of the
numbers is 2. Find the other number. 32
_
5.
29. The geometric mean of two numbers is 2 √
10
,
One of the numbers is 6. Find the other number. 3
Number Sense If the
average rate of return
in Exercise 40 were the
arithmetic mean, it would be 6.5%.
Unfortunately for the consumer, the
geometric mean of two numbers is
always smaller than the arithmetic
mean.
5 ft
_
or 3 1
3
Use the diagram to complete each equation.
x+y _
?
u
v
x =_
z y
_
31. _
32. _
30. _
z
u=xx+y
v = ? y
?
y
2
z
33. _ = _
34. (?) = y(x + y) v 35. u 2 = (x + y)(?) x
x z
?
Ý
Õ
Þ
â
Û
Give each answer in simplest radical form.
36. AD = 12, and CD = 8. Find BD. 4 √
6
Exercise 44 involves
using the geometric
mean corollaries
to find the lengths of a guy wire
anchor. This exercise prepares students for the Multi-Step Test Prep on
page 542.
37. AC = 16, and CD = 5. Find BC. 4 √
5
38. AD = CD = √
2 . Find BD.
, and AC = √
39. BC = √5
10 . Find CD.
41.
_ _
45. The area of the rect. is ab, and
the area of the square is s 2. It is
given that s 2 = ab, so s is the
geometric mean of a and b.
46. Let z be the geometric mean of x
and y, where x = a 2 and y = b 2.
2 2
b = ab, which is a
So z = √a
whole number.
52. Let AD = DC = a. By Corollary
8-1-3, AB 2 = (a)(2a) = 2a 2, and
BC 2 = (a)(2a) = 2a 2. So AB =
2 . Therefore ABC is
BC = a √
isosceles, so it is a 45°-45°-90°
triangle.
√
10
_
2
40. Finance An investment returns 3% one year and 10% the next year. The average
rate of return is the geometric mean of the two annual rates. What is the average rate
of return for this investment to the nearest tenth of a percent? 5.5%
41. B; the
proportion should
be 12 = EF .
EF
8
Answers
√
2
/////ERROR ANALYSIS///// Two students were asked to find EF.
Which solution is incorrect? Explain the error.
!
43. By Corollary 8-1-3,
a 2 = x(x + y),
and b 2 = y(x + y).
So a 2 + b 2 =
x(x + y) + y(x + y).
42.
By the Distrib.
Prop., this expression
simplifies to (x + y)
(x + y) = (x + y)2 43.
= c 2. So a 2 + b 2 = c 2.
"
£Ó
ÊÚÚÚ
ÊÊÊÊÊÊÚÚÚ
ÊÊÊÊ]ÊÜÊÊ
ÚÚÚ
ÊnÊÊÊÊÊÊÚÚÚ
ÊÊÊÊ]ÊÜÊÊ
n
Ó
Ê­®Ê ÊÊ­£Ó®­n®ÊʙȰÊÊ
Ê
е
/…ÕÃÊÊÊÊÊ ȖÊ ™ÈÊ
еÊ
Ê
Ê
еее
еÊ Ê°Ê Ê
ÊÊ{Ê
ÊȖÈÊ
ȖÊÊÊ­£È®­È®Ê
n
{
Ó
Ê­®Ê ÊÊ­n®­{®ÊÊÎÓ°ÊÊ
Ê
/…ÕÃÊÊÊÊÊ ȖÊ е
ÎÓÊ
еÊ
Ê
Ê
еее
еÊ Ê° Ê
ÊÊ{Ê
ÊȖÓÊ
ȖÊÊÊ­£È®­Ó®Ê
{
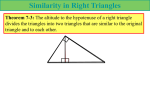
The altitude to the hypotenuse of a right triangle divides the hypotenuse into
segments that are 2 cm long and 5 cm long. Find the length of the altitude
to the nearest tenth of a centimeter. 3.2 cm
Critical Thinking Use the figure to show how
Corollary 8-1-3 can be used to derive the Pythagorean
Theorem. (Hint: Use the corollary to write expressions
for a 2 and b 2. Then add the expressions.)
Ý
V
>
Þ
L
44. This problem will prepare you for the Multi-Step Test Prep on page 542.
Before installing a utility pole, a crew must first
dig a hole and install the anchor for the guy wire
−−− −−
that supports the pole. In the diagram, SW ⊥ RT,
−−− −−−
RW ⊥ WT, RS = 4 ft, and ST = 3 ft.
−−−
a. Find the depth of the anchor SW to the
nearest inch. 3 ft 6 in.
−−−
b. Find the length of the rod RW to the nearest inch.
8-1 PRACTICE A
8-1 PRACTICE B
n‡£
3IMILARITYIN2IGHT4RIANGLES
522
7RITEASIMILARITYSTATEMENTCOMPARINGTHETHREETRIANGLESINEACHDIAGRAM
-
*
+
$
8
,%33/.
%
,
&
'
7
9
O$%&O'%$
O789O:87
O,+-
O'$&
O:79
AND
??
?????
q
AND
^
q
X
5
10
Z
Z
^
^
qqq
15
Y
6
X
^
ge07se_c08_0518_0523.indd $IAGRAMS
522
^
Y
X
27
%QUATIONS
4HELENGTHOFTHE
ALTITUDEISTHEGEOMETRIC
MEANOFTHELENGTHSOF
THETWOSEGMENTSOFTHE
HYPOTENUSE
Y
?? ??
B
H XY
A XC
B YC
H
Y
C
"
!
$
$
!
3
Z
^
^
"
#
4HEGEOMETRICMEANOFTWOPOSITIVENUMBERSISTHEPOSITIVESQUAREROOTOFTHEIRPRODUCT
&INDTHEGEOMETRICMEANOFAND
,ETXBETHEGEOMETRICMEAN
X C
B
$EFINITIONOFGEOMETRICMEAN
XISTHEGEOMETRIC
MEANOFAANDB
A ??
??
X
X
B
X AB
X 3IMPLIFY
X
&INDTHEPOSITIVESQUAREROOT
^
XqAB
2
5
X
9
10
X
7RITEASIMILARITYSTATEMENTCOMPARINGTHETHREETRIANGLESINEACHDIAGRAM
7
%XAMPLES
-
X
'
0
X X
X X
,
7HATPROPORTIONCANBEWRITTENTOFIND
THEVALUEOFX 1.3 mi
7HATEQUATIONCANBEWRITTENTOFIND
THEVALUEOFX B
A
C
E
D
??
X
??
X
&
.
O-.,O.0,O-0.
2
*
(
7HATEQUATIONCANBEWRITTENTOFIND
THEVALUEOFY &INDTHEGEOMETRICMEANOFEACHPAIROFNUMBERS)FNECESSARYGIVETHEANSWER
INSIMPLESTRADICALFORM
AND
3OLVEFORY
Y Y
AND
!DD
O&'(O&*'O'*(
9
X
X X
5SETHEFIGUREFOR%XERCISESn
(OWCANYOUFINDTHEVALUEOFC #
9/19/05 4:38:31 PM
"
5SETHEFIGUREFOR%XERCISESn
5SETHEDIAGRAMTOCOMPLETEEACHEQUATION
Chapter 8
A
#
$
3IMILARITYSTATEMENTN!"#N!$"N"$#
??
A
X ??
3OLVEFORX
D ???
??
A
C E
!
??
X ??
H
X X
FEET
E
C
Y
4HELENGTHOFALEGISTHEGEOMETRICMEANOF
THELENGTHOFTHESEGMENTOFTHEHYPOTENUSE
THATISCLOSESTTOTHATLEGANDTHELENGTHOFTHE
ENTIREHYPOTENUSE
18
qq
1.7 mi
D ?????
???
A
BC
ORIGINAL
TRIANGLE
3OISTHEGEOMETRICMEANOFAND
Y
!LTITUDESAND3IMILAR4RIANGLES
4HEALTITUDETOTHEHYPOTENUSEOFARIGHTTRIANGLEFORMSTWO
TRIANGLESTHATARESIMILARTOEACHOTHERANDTOTHEORIGINALTRIANGLE
X
Z
4HE#OAST'UARDHASSENTARESCUEHELICOPTERTORETRIEVE
PASSENGERSOFFADISABLEDSHIP4HESHIPHASCALLEDINITS
POSITIONASMILESFROMSHORE7HENTHEHELICOPTER
PASSESOVERABUOYTHATISKNOWNTOBEMILESFROM
SHORETHEANGLEFORMEDBYTHESHORETHEHELICOPTER
ANDTHEDISABLEDSHIPIS$ETERMINEWHAT
THEALTIMETERWOULDREADTOTHENEARESTFOOT
WHENTHEHELICOPTERISDIRECTLYABOVETHEBUOY
522
C
8-1 RETEACH
3IMILARITYIN2IGHT4RIANGLES
X
A
Y
H
0ROPORTIONS
X
n‡£
,EGAND(YPOTENUSE
^
^
qq
Y
Z
3
^
25
65
Z
^
20
^
,iÌi>V…
,%33/.
B
AND
qq
q qq
C
E ???
??
E
B
!LTITUDEAND
(YPOTENUSE
qi
6
Y
7
^
8-1 READING STRATEGIES
5SEA4ABLE
7ORDS
X
,i>`ˆ˜}Ê-ÌÀ>Ìi}ˆiÃ
X
^
q
&INDXYANDZ
Y
n‡£
5SETHETABLEBELOWTOUNDERSTANDTHERELATIONSHIPSFORMEDWHENTHEALTITUDE
ISDRAWNFROMTHEVERTEXOFARIGHTTRIANGLETOITSHYPOTENUSE
"
&INDTHEGEOMETRICMEANOFEACHPAIROFNUMBERS)FNECESSARYGIVETHE
ANSWERINSIMPLESTRADICALFORM
AND
??
AND
AND
^
7
Chapter 8 Right Triangles and Trigonometry
:
0OSSIBLEANSWERS
O*+,O*,-
/
5 ft 3 in.
8-1 PRACTICE C
-
*À>V̈ViÊ
,%33/.
,
C
Y
AND
AND
^
q
^
q