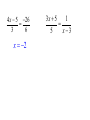* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Proportions and Similarity
Survey
Document related concepts
Transcript
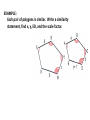
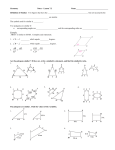
Advanced Geometry Similarity Lesson 2 Proportions & Similarity Ratio a b The ratio of a to b can be expressed as , where b is not zero. FORMS: 1 to 2 1: 2 1 2 All ratios must be in simplest form. 24 3 8 1 32 : 6 16 : 3 A ratio in which the denominator is 1 is called a unit ratio. EXAMPLE: The number of students that participate in sports programs at Central High School is 550. The total number of students in the school is 1850. Find the athlete to non-athlete ratio. 4 x 5 26 3 6 x 2 3x 5 1 5 x3 An extended ratio is a ratio used to compare three or more numbers. Extended ratios are written using colons. EXAMPLE: In a triangle, the ratio of the measures of three angles is 1 1 1 : : . Find the measures of the angles of the triangle. 3 4 6 Example: The ratios of the sides of three polygons are given. Make a conjecture about the type of each polygon described. 2:2:3 3: 3: 3: 3 Isosceles triangle Rhombus 4:5:4:5 Similar Polygons In order for two polygons to be similar, all of their corresponding angles must be congruent and all of the corresponding sides must form a proportion. A B D F C E Similarity Statement: A E B F C D AB BC AC EF FD ED EXAMPLES: Determine whether each pair of figures is similar. Justify your answer. No; the corresponding angles are not congruent. EXAMPLE: An architect prepared a 12-inch model of a skyscraper to look like an actual 1100-foot building. What is the scale factor of the model compared to the actual building? EXAMPLE: Each pair of polygons is similar. Write a similarity statement, find x, y, ED, and the scale factor.